二维圆柱绕流
本案例要求MindSpore版本 >= 2.0.0调用如下接口: mindspore.jit，mindspore.jit_class，mindspore.jacrev。
概述
圆柱绕流，是指二维圆柱低速定常绕流的流型只与Re数有关。在Re≤1时，流场中的惯性力与粘性力相比居次要地位，圆柱上下游的流线前后对称，阻力系数近似与Re成反比，此Re数范围的绕流称为斯托克斯区；随着Re的增大，圆柱上下游的流线逐渐失去对称性。这种特殊的现象反映了流体与物体表面相互作用的奇特本质，求解圆柱绕流则是流体力学中的经典问题。
由于控制方程纳维-斯托克斯方程（Navier-Stokes equation）难以得到泛化的理论解，使用数值方法对圆柱绕流场景下控制方程进行求解，从而预测流场的流动，成为计算流体力学中的样板问题。传统求解方法通常需要对流体进行精细离散化，以捕获需要建模的现象。因此，传统有限元法（finite element method，FEM）和有限差分法（finite difference method，FDM）往往成本比较大。
物理启发的神经网络方法（Physics-informed Neural Networks），以下简称PINNs，通过使用逼近控制方程的损失函数以及简单的网络构型，为快速求解复杂流体问题提供了新的方法。本案例利用神经网络数据驱动特性，结合PINNs求解圆柱绕流问题。
问题描述
纳维-斯托克斯方程（Navier-Stokes equation），简称N-S方程，是流体力学领域的经典偏微分方程，在粘性不可压缩情况下，无量纲N-S方程的形式如下：
\[\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0\]
\[\frac{\partial u} {\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = - \frac{\partial p}{\partial x} + \frac{1} {Re} (\frac{\partial^2u}{\partial x^2} + \frac{\partial^2u}{\partial y^2})\]
\[\frac{\partial v} {\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} = - \frac{\partial p}{\partial y} + \frac{1} {Re} (\frac{\partial^2v}{\partial x^2} + \frac{\partial^2v}{\partial y^2})\]
其中，Re表示雷诺数。
本案例利用PINNs方法学习位置和时间到相应流场物理量的映射，实现N-S方程的求解：
\[(x, y, t) \mapsto (u, v, p)\]
技术路径
MindSpore Flow求解该问题的具体流程如下：
创建数据集。
构建模型。
自适应损失的多任务学习。
优化器。
NavierStokes2D。
模型训练。
模型推理及可视化。
[1]:
import time
import numpy as np
import mindspore
from mindspore import nn, ops, Tensor, jit, set_seed, load_checkpoint, load_param_into_net
from mindspore import dtype as mstype
下述src包可以在applications/physics_driven/navier_stokes/cylinder_flow_forward/src下载。
[2]:
from mindflow.cell import MultiScaleFCCell
from mindflow.loss import MTLWeightedLossCell
from mindflow.pde import NavierStokes, sympy_to_mindspore
from mindflow.utils import load_yaml_config
from src import create_training_dataset, create_test_dataset, calculate_l2_error
set_seed(123456)
np.random.seed(123456)
[3]:
# set context for training: using graph mode for high performance training with GPU acceleration
config = load_yaml_config('cylinder_flow.yaml')
mindspore.set_context(mode=mindspore.GRAPH_MODE, device_target="GPU", device_id=3)
use_ascend = mindspore.get_context(attr_key='device_target') == "Ascend"
创建数据集
本案例对已有的雷诺数为100的标准圆柱绕流进行初始条件和边界条件数据的采样。对于训练数据集，构建平面矩形的问题域以及时间维度，再对已知的初始条件，边界条件采样；基于已有的流场中的点构造测试集。
下载训练与测试数据集：physics_driven/flow_past_cylinder/dataset。
[4]:
# create training dataset
cylinder_flow_train_dataset = create_training_dataset(config)
cylinder_dataset = cylinder_flow_train_dataset.create_dataset(batch_size=config["train_batch_size"],
shuffle=True,
prebatched_data=True,
drop_remainder=True)
# create test dataset
inputs, label = create_test_dataset(config["test_data_path"])
./dataset
get dataset path: ./dataset
check eval dataset length: (36, 100, 50, 3)
构建模型
本示例使用一个简单的全连接网络，深度为6层，激活函数是tanh函数。
[5]:
coord_min = np.array(config["geometry"]["coord_min"] + [config["geometry"]["time_min"]]).astype(np.float32)
coord_max = np.array(config["geometry"]["coord_max"] + [config["geometry"]["time_max"]]).astype(np.float32)
input_center = list(0.5 * (coord_max + coord_min))
input_scale = list(2.0 / (coord_max - coord_min))
model = MultiScaleFCCell(in_channels=config["model"]["in_channels"],
out_channels=config["model"]["out_channels"],
layers=config["model"]["layers"],
neurons=config["model"]["neurons"],
residual=config["model"]["residual"],
act='tanh',
num_scales=1,
input_scale=input_scale,
input_center=input_center)
自适应损失的多任务学习
同一时间，基于PINNs的方法需要优化多个loss，给优化过程带来的巨大的挑战。我们采用Kendall, Alex, Yarin Gal, and Roberto Cipolla. “Multi-task learning using uncertainty to weigh losses for scene geometry and semantics.” CVPR, 2018. 论文中提出的不确定性权重算法动态调整权重。
[6]:
mtl = MTLWeightedLossCell(num_losses=cylinder_flow_train_dataset.num_dataset)
优化器
[7]:
if config["load_ckpt"]:
param_dict = load_checkpoint(config["load_ckpt_path"])
load_param_into_net(model, param_dict)
load_param_into_net(mtl, param_dict)
# define optimizer
params = model.trainable_params() + mtl.trainable_params()
optimizer = nn.Adam(params, config["optimizer"]["initial_lr"])
模型训练
使用MindSpore >= 2.0.0的版本，可以使用函数式编程范式训练神经网络。
[9]:
def train():
problem = NavierStokes2D(model)
from mindspore.amp import DynamicLossScaler, auto_mixed_precision, all_finite
if use_ascend:
loss_scaler = DynamicLossScaler(1024, 2, 100)
auto_mixed_precision(model, 'O3')
else:
loss_scaler = None
# the loss function receives 5 data sources: pde, ic, ic_label, bc and bc_label
def forward_fn(pde_data, bc_data, bc_label, ic_data, ic_label):
loss = problem.get_loss(pde_data, bc_data, bc_label, ic_data, ic_label)
if use_ascend:
loss = loss_scaler.scale(loss)
return loss
grad_fn = mindspore.value_and_grad(forward_fn, None, optimizer.parameters, has_aux=False)
# using jit function to accelerate training process
@jit
def train_step(pde_data, bc_data, bc_label, ic_data, ic_label):
loss, grads = grad_fn(pde_data, bc_data, bc_label, ic_data, ic_label)
if use_ascend:
loss = loss_scaler.unscale(loss)
if all_finite(grads):
grads = loss_scaler.unscale(grads)
loss = ops.depend(loss, optimizer(grads))
return loss
epochs = config["train_epochs"]
steps_per_epochs = cylinder_dataset.get_dataset_size()
sink_process = mindspore.data_sink(train_step, cylinder_dataset, sink_size=1)
for epoch in range(1, 1 + epochs):
# train
time_beg = time.time()
model.set_train(True)
for _ in range(steps_per_epochs + 1):
step_train_loss = sink_process()
print(f"epoch: {epoch} train loss: {step_train_loss} epoch time: {(time.time() - time_beg)*1000 :.3f} ms")
model.set_train(False)
if epoch % config["eval_interval_epochs"] == 0:
# eval
calculate_l2_error(model, inputs, label, config)
[10]:
time_beg = time.time()
train()
print("End-to-End total time: {} s".format(time.time() - time_beg))
momentum_x: u(x, y, t)*Derivative(u(x, y, t), x) + v(x, y, t)*Derivative(u(x, y, t), y) + Derivative(p(x, y, t), x) + Derivative(u(x, y, t), t) - 0.00999999977648258*Derivative(u(x, y, t), (x, 2)) - 0.00999999977648258*Derivative(u(x, y, t), (y, 2))
Item numbers of current derivative formula nodes: 6
momentum_y: u(x, y, t)*Derivative(v(x, y, t), x) + v(x, y, t)*Derivative(v(x, y, t), y) + Derivative(p(x, y, t), y) + Derivative(v(x, y, t), t) - 0.00999999977648258*Derivative(v(x, y, t), (x, 2)) - 0.00999999977648258*Derivative(v(x, y, t), (y, 2))
Item numbers of current derivative formula nodes: 6
continuty: Derivative(u(x, y, t), x) + Derivative(v(x, y, t), y)
Item numbers of current derivative formula nodes: 2
ic_u: u(x, y, t)
Item numbers of current derivative formula nodes: 1
ic_v: v(x, y, t)
Item numbers of current derivative formula nodes: 1
ic_p: p(x, y, t)
Item numbers of current derivative formula nodes: 1
bc_u: u(x, y, t)
Item numbers of current derivative formula nodes: 1
bc_v: v(x, y, t)
Item numbers of current derivative formula nodes: 1
epoch: 100 train loss: 0.093663074 epoch time: 865.762 ms
predict total time: 311.9645118713379 ms
l2_error, U: 0.3021394710211443 , V: 1.000814785933711 , P: 0.7896103436562808 , Total: 0.4195581394947756
==================================================================================================
epoch: 200 train loss: 0.051423326 epoch time: 862.246 ms
predict total time: 22.994279861450195 ms
l2_error, U: 0.17839493992645483 , V: 1.0002689685398058 , P: 0.7346766341097746 , Total: 0.34769129318171776
==================================================================================================
epoch: 300 train loss: 0.048922822 epoch time: 862.698 ms
predict total time: 20.47276496887207 ms
l2_error, U: 0.19347126434977727 , V: 0.9995530930847041 , P: 0.7544902230473761 , Total: 0.35548966915028823
==================================================================================================
epoch: 400 train loss: 0.045927174 epoch time: 864.443 ms
predict total time: 21.65961265563965 ms
l2_error, U: 0.1824223402341706 , V: 0.9989275825381772 , P: 0.7425240152913066 , Total: 0.3495656434506572
==================================================================================================
...
epoch: 11600 train loss: 0.00017444199 epoch time: 865.210 ms
predict total time: 24.872541427612305 ms
l2_error, U: 0.014519163118953455 , V: 0.05904803878272691 , P: 0.06563451497967088 , Total: 0.023605441537703505
==================================================================================================
epoch: 11700 train loss: 0.00010273233 epoch time: 862.965 ms
predict total time: 26.495933532714844 ms
l2_error, U: 0.015113672755658001 , V: 0.06146986437422137 , P: 0.06977751959988018 , Total: 0.024650437825199538
==================================================================================================
epoch: 11800 train loss: 9.145654e-05 epoch time: 861.971 ms
predict total time: 26.30162239074707 ms
l2_error, U: 0.014403110291772709 , V: 0.056214072467378313 , P: 0.06351121097459393 , Total: 0.02285192095148332
==================================================================================================
epoch: 11900 train loss: 5.3686792e-05 epoch time: 862.390 ms
predict total time: 25.954484939575195 ms
l2_error, U: 0.015531273782397546 , V: 0.059835203301053276 , P: 0.07341694396502277 , Total: 0.02475477793452502
==================================================================================================
epoch: 12000 train loss: 4.5837318e-05 epoch time: 860.097 ms
predict total time: 25.703907012939453 ms
l2_error, U: 0.014675419283356958 , V: 0.05753859917060074 , P: 0.06372057740590953 , Total: 0.02328489716397064
==================================================================================================
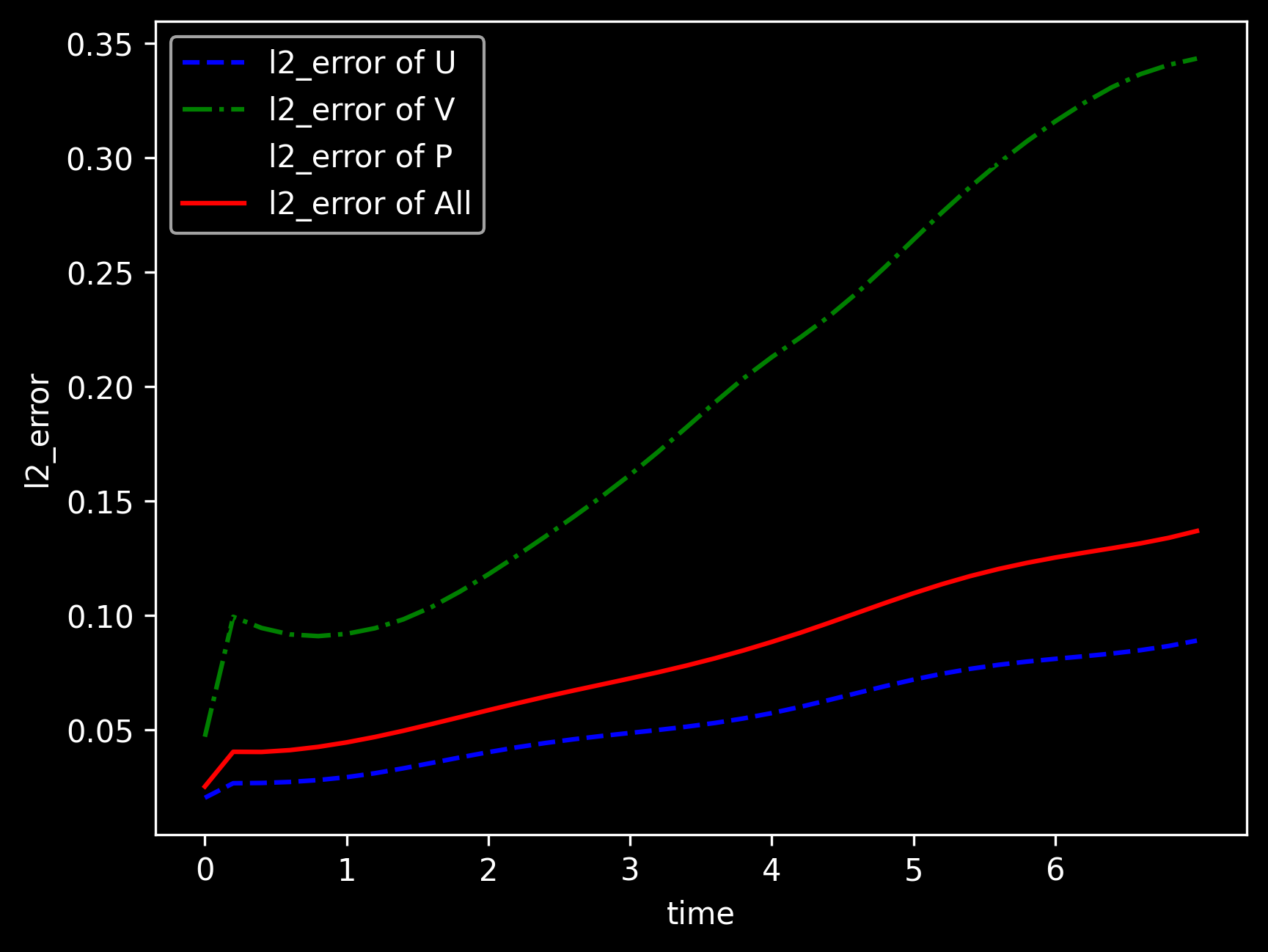
模型推理及可视化
训练后可对流场内所有数据点进行推理，并可视化相关结果。
[11]:
from src import visual
# visualization
visual(model=model, epochs=config["train_epochs"], input_data=inputs, label=label)
