基于KNO求解二维Navier-Stokes
概述
计算流体力学是21世纪流体力学领域的重要技术之一,其通过使用数值方法在计算机中对流体力学的控制方程进行求解,从而实现流动的分析、预测和控制。传统的有限元法(finite element method,FEM)和有限差分法(finite difference method,FDM)常用于复杂的仿真流程(物理建模、网格划分、数值离散、迭代求解等)和较高的计算成本,往往效率低下。因此,借助AI提升流体仿真效率是十分必要的。
近年来,随着神经网络的迅猛发展,为科学计算提供了新的范式。经典的神经网络是在有限维度的空间进行映射,只能学习与特定离散化相关的解。与经典神经网络不同,傅里叶神经算子(Fourier Neural Operator,FNO)是一种能够学习无限维函数空间映射的新型深度学习架构。该架构可直接学习从任意函数参数到解的映射,用于解决一类偏微分方程的求解问题,具有更强的泛化能力。更多信息可参考Fourier Neural Operator for Parametric Partial Differential Equations。
但是这类神经算子在学习非线性PDE的长期行为时,变得不够准确和缺乏可解释性。库普曼神经算子(Koopman neural operator,KNO)通过构建方程解的非线性动力学系统,克服了这一问题。通过近似Koopman算子,一个控制动力学系统所有可能观测的无限维线性算子,作用于动力学系统的流映射,我们可以通过求解简单的线性预测问题等价地学习整个非线性PDE族的解。更多信息可参考:
“Koopman neural operator as a mesh-free solver of non-linear partial differential equations.” arXiv preprint arXiv:2301.10022 (2023).
“KoopmanLab: machine learning for solving complex physics equations.” arXiv preprint arXiv:2301.01104 (2023).
本案例教程介绍利用库普曼神经算子的纳维-斯托克斯方程(Navier-Stokes equation)求解方法。
纳维-斯托克斯方程(Navier-Stokes equation)
纳维-斯托克斯方程(Navier-Stokes equation)是计算流体力学领域的经典方程,是一组描述流体动量守恒的偏微分方程,简称N-S方程。它在二维不可压缩流动中的涡度形式如下:
其中\(u\)表示速度场,\(w=\nabla \times u\)表示涡度,\(w_0(x)\)表示初始条件,\(\nu\)表示粘度系数,\(f(x)\)为外力合力项。
问题描述
本案例利用Koopman Neural Operator学习某一个时刻对应涡度到下一时刻涡度的映射,实现二维不可压缩N-S方程的求解:
技术路径
MindSpore Flow求解该问题的具体流程如下:
创建数据集。
构建模型。
优化器与损失函数。
模型训练。
模型推理和可视化。
Koopman Neural Operator
Koopman Neural Operator模型构架如下图所示,包含上下两个主要分支和对应输出。图中Input表示初始涡度,上路分支通过Encoding Layer实现输入向量的高维映射,然后将映射结果作为Koopman Layer的输入,进行频域信息的非线性变换,最后由Decoding Layer将变换结果映射至最终的预测结果Prediction。同时,下路分支通过Encoding Layer实现输入向量的高维映射,然后通过Decoding Layer对输入进行重建。上下两个分支的Encoding Layer之间共享权重,Decoding Layer之间也共享权重。Prediction用于和Label计算预测误差,Reconstruction用于和Input计算重建误差。两个误差共同指导模型的梯度计算。
Encoding Layer、Koopman Layer、Decoding Layer以及两分支共同组成了Koopman Neural Operator。
Koopman Layer网络结构如虚线框所示,可重复堆叠。向量经过傅里叶变换后,经过线性变换,过滤高频信息,然后进行傅里叶逆变换;输出结果与输入相加,最后通过激活函数,得到输出向量。

[2]:
import os
import time
import datetime
import numpy as np
import mindspore
from mindspore import nn, context, ops, Tensor, set_seed, dtype
from mindspore.nn import MSELoss
from mindflow.cell import KNO2D
from mindflow.common import get_warmup_cosine_annealing_lr
from mindflow.utils import load_yaml_config
下述src包可以在applications/data_driven/navier_stokes/kno2d/src下载。
[3]:
from src.dataset import create_training_dataset
from src.trainer import NavierStokesWithLoss
from src.utils import visual
set_seed(0)
np.random.seed(0)
print("pid:", os.getpid())
print(datetime.datetime.now())
context.set_context(mode=context.GRAPH_MODE, device_target='Ascend', device_id=4)
use_ascend = context.get_context(attr_key='device_target') == "Ascend"
pid: 184534
2023-03-04 07:39:18.207815
从config中获得模型、数据、优化器的超参。
[4]:
config = load_yaml_config('navier_stokes_2d.yaml')
data_params = config["data"]
model_params = config["model"]
optimizer_params = config["optimizer"]
创建数据集
训练与测试数据下载: data_driven/navier_stokes/dataset。
本案例根据Zongyi Li在 Fourier Neural Operator for Parametric Partial Differential Equations 一文中对数据集的设置生成训练数据集与测试数据集。具体设置如下:
基于周期性边界,生成满足如下分布的初始条件\(w_0(x)\):
外力项设置为:
采用Crank-Nicolson方法生成数据,时间步长设置为1e-4,最终数据以每 t = 1 个时间单位记录解。所有数据均在256×256的网格上生成,并被下采样至64×64网格。本案例选取粘度系数\(\nu=1e−5\),训练集样本量为19000个,测试集样本量为3800个。
[5]:
# create training dataset
train_dataset = create_training_dataset(data_params, shuffle=True)
test_input = np.load(os.path.join(data_params["path"], "test/inputs.npy"))
test_label = np.load(os.path.join(data_params["path"], "test/label.npy"))
print('test_input: ', test_input.shape)
print('test_label: ', test_label.shape)
Data preparation finished
input_path: (19000, 64, 64, 1, 1)
label_path: (19000, 64, 64, 1, 1)
test_input: (200, 19, 64, 64, 1, 1)
test_label: (200, 19, 64, 64, 1, 1)
构建模型
网络由1层共享的Encoding Layer、多层Koopman Layer以及1层共享的Decoding Layer叠加组成:
Encoding Layer对应样例代码中
KNO2D.enc,将输出数据映射至高维;Koopman Layer对应样例代码中
KNO2D.koopman_layer,本案例采用离散傅里叶变换实现时域与频域的转换;Decoding Layer对应代码中
KNO2D.dec,获得最终的预测值。
[6]:
model = KNO2D(in_channels=data_params['in_channels'],
channels=model_params['channels'],
modes=model_params['modes'],
depths=model_params['depths'],
resolution=model_params['resolution'],
compute_dtype=dtype.float16 if use_ascend else dtype.float32
)
model_params_list = []
for k, v in model_params.items():
model_params_list.append(f"{k}:{v}")
model_name = "_".join(model_params_list)
print(model_name)
name:KNO2D_channels:20_modes:16_depths:4_resolution:64
优化器与损失函数
使用均方误差作为网络训练损失函数:
[7]:
train_size = train_dataset.get_dataset_size()
lr = get_warmup_cosine_annealing_lr(lr_init=optimizer_params["lr"],
last_epoch=optimizer_params["epochs"],
steps_per_epoch=train_size,
warmup_epochs=1)
optimizer = nn.AdamWeightDecay(model.trainable_params(),
learning_rate=Tensor(lr),
weight_decay=optimizer_params["weight_decay"])
model.set_train()
loss_fn = MSELoss()
if use_ascend:
from mindspore.amp import DynamicLossScaler, auto_mixed_precision, all_finite
loss_scaler = DynamicLossScaler(1024, 2, 100)
auto_mixed_precision(model, 'O3')
else:
loss_scaler = None
模型训练
使用MindSpore >= 2.0.0的版本,可以使用函数式编程范式训练神经网络。
[8]:
problem = NavierStokesWithLoss(model, data_params["out_channels"], loss_fn, data_format="NHWTC")
def forward_fn(inputs, labels):
loss, l_recons, l_pred = problem.get_loss(inputs, labels)
if use_ascend:
loss = loss_scaler.scale(loss)
return loss, l_recons, l_pred
grad_fn = ops.value_and_grad(forward_fn, None, optimizer.parameters, has_aux=True)
def train_step(inputs, labels):
(loss, l_recons, l_pred), grads = grad_fn(inputs, labels)
if use_ascend:
loss = loss_scaler.unscale(loss)
if all_finite(grads):
grads = loss_scaler.unscale(grads)
loss = ops.depend(loss, optimizer(grads))
return loss, l_recons, l_pred
train_sink = mindspore.data_sink(train_step, train_dataset, sink_size=1)
summary_dir = os.path.join(config["summary_dir"], model_name)
os.makedirs(summary_dir, exist_ok=True)
print(summary_dir)
for epoch in range(1, optimizer_params["epochs"] + 1):
time_beg = time.time()
train_recons_full = 0.0
train_pred_full = 0.0
for _ in range(train_size):
_, l_recons, l_pred = train_sink()
train_recons_full += l_recons.asnumpy()
train_pred_full += l_pred.asnumpy()
train_recons_full = train_recons_full / train_size
train_pred_full = train_pred_full / train_size
print(f"epoch: {epoch}, time cost: {(time.time() - time_beg):>8f},"
f" recons loss: {train_recons_full:>8f}, pred loss: {train_pred_full:>8f}")
if epoch % config['eval_interval'] == 0:
l_recons_all, l_pred_all = problem.test(test_input, test_label)
print(f'Eval epoch: {epoch}, recons loss: {l_recons_all}, relative pred loss: {l_pred_all}')
mindspore.save_checkpoint(model, ckpt_file_name=summary_dir + '/save_model.ckpt')
./summary_dir/name:KNO2D_channels:20_modes:16_depths:4_resolution:64
epoch: 1, time cost: 55.562426, recons loss: 0.467314, pred loss: 0.237300
epoch: 2, time cost: 32.804436, recons loss: 0.175188, pred loss: 0.050888
epoch: 3, time cost: 32.946971, recons loss: 0.167865, pred loss: 0.041778
epoch: 4, time cost: 33.064430, recons loss: 0.170181, pred loss: 0.038075
epoch: 5, time cost: 32.907211, recons loss: 0.171853, pred loss: 0.035849
epoch: 6, time cost: 33.799230, recons loss: 0.173322, pred loss: 0.034017
epoch: 7, time cost: 32.612255, recons loss: 0.174376, pred loss: 0.032719
epoch: 8, time cost: 32.896673, recons loss: 0.175445, pred loss: 0.031596
epoch: 9, time cost: 33.907305, recons loss: 0.176131, pred loss: 0.030644
epoch: 10, time cost: 33.175130, recons loss: 0.176701, pred loss: 0.029969
Eval epoch: 10, recons loss: 0.23137304687500002, relative pred loss: 0.03798459614068269
...
epoch: 41, time cost: 32.962233, recons loss: 0.185430, pred loss: 0.017872
epoch: 42, time cost: 33.296847, recons loss: 0.185595, pred loss: 0.017749
epoch: 43, time cost: 33.803700, recons loss: 0.185646, pred loss: 0.017651
epoch: 44, time cost: 32.776349, recons loss: 0.185723, pred loss: 0.017564
epoch: 45, time cost: 33.377666, recons loss: 0.185724, pred loss: 0.017497
epoch: 46, time cost: 33.228983, recons loss: 0.185827, pred loss: 0.017434
epoch: 47, time cost: 33.244342, recons loss: 0.185854, pred loss: 0.017393
epoch: 48, time cost: 33.211263, recons loss: 0.185912, pred loss: 0.017361
epoch: 49, time cost: 35.656644, recons loss: 0.185897, pred loss: 0.017349
epoch: 50, time cost: 33.527458, recons loss: 0.185899, pred loss: 0.017344
Eval epoch: 50, recons loss: 0.2389616699218751, relative pred loss: 0.03355878115445375
模型推理和可视化
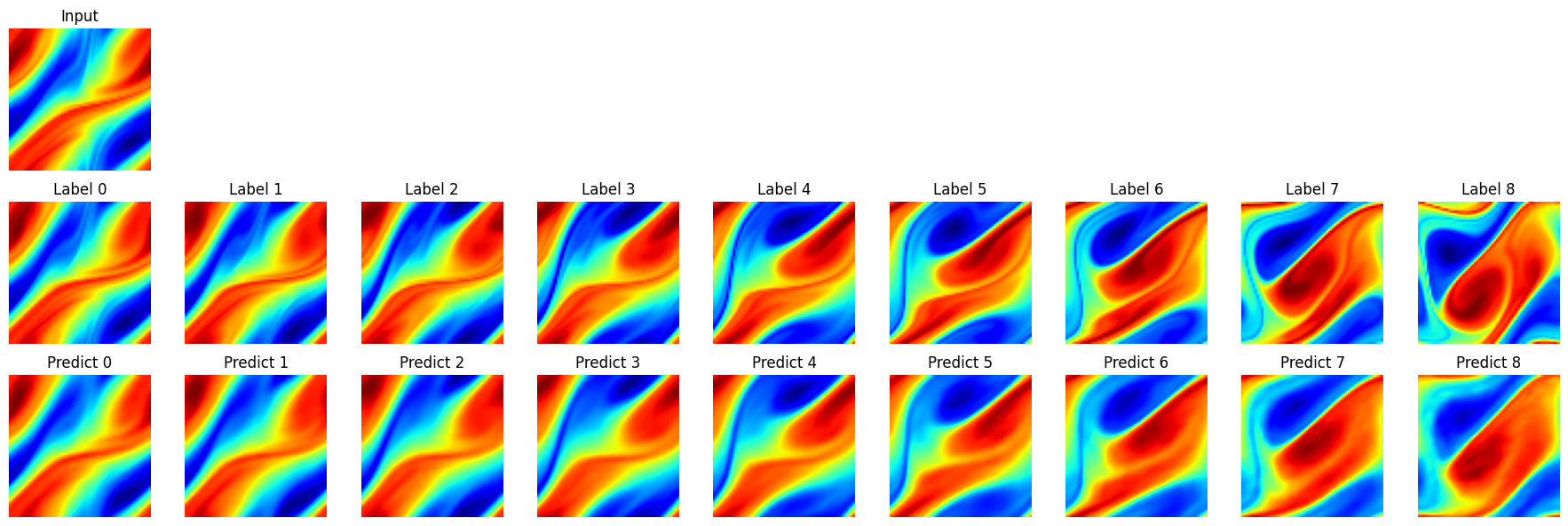
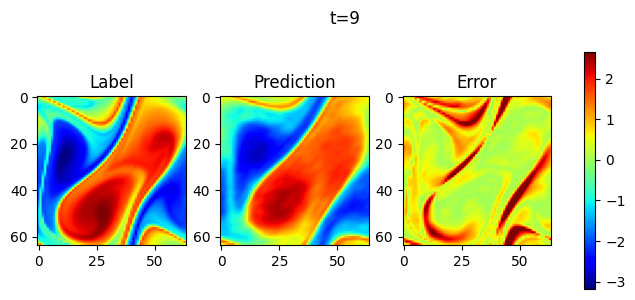
取1个样本做连续10步预测,并可视化。
[13]:
# Infer and plot some data.
visual(problem, test_input, test_label, t_out=10)