使用PINNs求解Kovasznay流问题
问题描述
本案例演示如何利用PINNs求解Kovasznay流问题。Kovasznay流是Navier-Stokes(N-S)方程的一个特定条件下的解析解。Kovasznay流满足N-S方程的动量方程和连续性方程,并且满足Dirichlet边界条件。
Kovasznay流的速度和压力分布可以表示为以下公式:
\[u=1-e^{\lambda x}\cos{(2\pi y)}.\]
\[v=\frac{\lambda}{2\pi}e^{\lambda x}\sin(2\pi x).\]
\[p = \frac{1}{2}(1-e^{2\lambda x}).\]
其中,\(\lambda=\frac{1}{2\nu}-\sqrt{\frac{1}{4\nu^2}+4\pi^2}\)。
我们可以将Kovasznay流作为一个基准解,用于验证PINNs方法的准确性和稳定性。
技术路径
MindSpore Flow求解该问题的具体流程如下:
创建训练数据集。
构建模型。
优化器。
约束。
模型训练。
模型评估。
[1]:
import time
from mindspore import context, nn, ops, jit
from mindflow import load_yaml_config
from mindflow.cell import FCSequential
from mindflow.loss import get_loss_metric
from mindspore import load_checkpoint, load_param_into_net, save_checkpoint
from src.dataset import create_dataset
context.set_context(mode=context.GRAPH_MODE, save_graphs=False, device_target="GPU")
# Load config
file_cfg = "kovasznay_cfg.yaml"
config = load_yaml_config(file_cfg)
创建数据集
本案例在求解域及边值条件进行随机采样,生成训练数据集与测试数据集。具体方法见src/dataset.py。
[2]:
ds_train = create_dataset(config)
构建模型
本示例使用一个简单的全连接网络,深度为4层,每层的神经元个数为50,激活函数为tanh。
[3]:
model = FCSequential(
in_channels=config["model"]["in_channels"],
out_channels=config["model"]["out_channels"],
layers=config["model"]["layers"],
neurons=config["model"]["neurons"],
residual=config["model"]["residual"],
act="tanh",
)
[4]:
if config["load_ckpt"]:
param_dict = load_checkpoint(config["load_ckpt_path"])
load_param_into_net(model, param_dict)
params = model.trainable_params()
optimizer = nn.Adam(params, learning_rate=config["optimizer"]["initial_lr"])
Kovasznay 求解器
下述Kovasznay将作为约束条件,用于求解Kovasznay流问题。 包含两个部分,分别为Kovasznay流方程和边界条件。
边界条件根据上述参考解进行设置。
[5]:
import sympy
from sympy import Function, diff, symbols
from mindspore import numpy as ms_np
from mindflow import PDEWithLoss, sympy_to_mindspore
import math
class Kovasznay(PDEWithLoss):
"""Define the loss of the Kovasznay flow."""
def __init__(self, model, re=20, loss_fn=nn.MSELoss()):
"""Initialize."""
self.re = re
self.nu = 1 / self.re
self.l = 1 / (2 * self.nu) - math.sqrt(
1 / (4 * self.nu**2) + 4 * math.pi**2
)
self.x, self.y = symbols("x y")
self.u = Function("u")(self.x, self.y)
self.v = Function("v")(self.x, self.y)
self.p = Function("p")(self.x, self.y)
self.in_vars = [self.x, self.y]
self.out_vars = [self.u, self.v, self.p]
super(Kovasznay, self).__init__(model, self.in_vars, self.out_vars)
self.bc_nodes = sympy_to_mindspore(self.bc(), self.in_vars, self.out_vars)
if isinstance(loss_fn, str):
self.loss_fn = get_loss_metric(loss_fn)
else:
self.loss_fn = loss_fn
def pde(self):
"""Define the gonvering equation."""
u, v, p = self.out_vars
u_x = diff(u, self.x)
u_y = diff(u, self.y)
v_x = diff(v, self.x)
v_y = diff(v, self.y)
p_x = diff(p, self.x)
p_y = diff(p, self.y)
u_xx = diff(u_x, self.x)
u_yy = diff(u_y, self.y)
v_xx = diff(v_x, self.x)
v_yy = diff(v_y, self.y)
momentum_x = u * u_x + v * u_y + p_x - (1 / self.re) * (u_xx + u_yy)
momentum_y = u * v_x + v * v_y + p_y - (1 / self.re) * (v_xx + v_yy)
continuty = u_x + v_y
equations = {
"momentum_x": momentum_x,
"momentum_y": momentum_y,
"continuty": continuty,
}
return equations
def u_func(self):
"""Define the analytical solution."""
u = 1 - sympy.exp(self.l * self.x) * sympy.cos(2 * sympy.pi * self.y)
return u
def v_func(self):
"""Define the analytical solution."""
v = (
self.l
/ (2 * sympy.pi)
* sympy.exp(self.l * self.x)
* sympy.sin(2 * sympy.pi * self.y)
)
return v
def p_func(self):
"""Define the analytical solution."""
p = 1 / 2 * (1 - sympy.exp(2 * self.l * self.x))
return p
def bc(self):
"""Define the boundary condition."""
bc_u = self.u - self.u_func()
bc_v = self.v - self.v_func()
bc_p = self.p - self.p_func()
bcs = {"u": bc_u, "v": bc_v, "p": bc_p}
return bcs
def get_loss(self, pde_data, bc_data):
"""Define the loss function."""
pde_res = self.parse_node(self.pde_nodes, inputs=pde_data)
pde_residual = ops.Concat(axis=1)(pde_res)
pde_loss = self.loss_fn(pde_residual, ms_np.zeros_like(pde_residual))
bc_res = self.parse_node(self.bc_nodes, inputs=bc_data)
bc_residual = ops.Concat(axis=1)(bc_res)
bc_loss = self.loss_fn(bc_residual, ms_np.zeros_like(bc_residual))
return pde_loss + bc_loss
# Create the problem
problem = Kovasznay(model)
momentum_x: u(x, y)*Derivative(u(x, y), x) + v(x, y)*Derivative(u(x, y), y) + Derivative(p(x, y), x) - 0.05*Derivative(u(x, y), (x, 2)) - 0.05*Derivative(u(x, y), (y, 2))
Item numbers of current derivative formula nodes: 5
momentum_y: u(x, y)*Derivative(v(x, y), x) + v(x, y)*Derivative(v(x, y), y) + Derivative(p(x, y), y) - 0.05*Derivative(v(x, y), (x, 2)) - 0.05*Derivative(v(x, y), (y, 2))
Item numbers of current derivative formula nodes: 5
continuty: Derivative(u(x, y), x) + Derivative(v(x, y), y)
Item numbers of current derivative formula nodes: 2
u: u(x, y) - 1 + exp(-1.81009812001397*x)*cos(2*pi*y)
Item numbers of current derivative formula nodes: 3
v: v(x, y) + 0.905049060006983*exp(-1.81009812001397*x)*sin(2*pi*y)/pi
Item numbers of current derivative formula nodes: 2
p: p(x, y) - 0.5 + 0.5*exp(-3.62019624002793*x)
Item numbers of current derivative formula nodes: 3
模型训练
使用MindSpore>= 2.0.0的版本,可以使用函数式编程范式训练神经网络。
[6]:
def train(config):
grad_fn = ops.value_and_grad(
problem.get_loss, None, optimizer.parameters, has_aux=False
)
@jit
def train_step(pde_data, bc_data):
loss, grads = grad_fn(pde_data, bc_data)
loss = ops.depend(loss, optimizer(grads))
return loss
def train_epoch(model, dataset, i_epoch):
model.set_train()
n_step = dataset.get_dataset_size()
for i_step, (pde_data, bc_data) in enumerate(dataset):
local_time_beg = time.time()
loss = train_step(pde_data, bc_data)
if i_step % 50 == 0:
print(
"\repoch: {}, loss: {:>f}, time elapsed: {:.1f}ms [{}/{}]".format(
i_epoch,
float(loss),
(time.time() - local_time_beg) * 1000,
i_step + 1,
n_step,
)
)
for i_epoch in range(config["epochs"]):
train_epoch(model, ds_train, i_epoch)
if config["save_ckpt"]:
save_checkpoint(model, config["save_ckpt_path"])
[7]:
time_beg = time.time()
train(config)
print("End-to-End total time: {} s".format(time.time() - time_beg))
epoch: 0, loss: 0.239163, time elapsed: 9470.9ms [1/125]
epoch: 0, loss: 0.087055, time elapsed: 44.7ms [51/125]
epoch: 0, loss: 0.086475, time elapsed: 45.2ms [101/125]
epoch: 1, loss: 0.085488, time elapsed: 47.1ms [1/125]
epoch: 1, loss: 0.087387, time elapsed: 45.5ms [51/125]
epoch: 1, loss: 0.083520, time elapsed: 45.2ms [101/125]
epoch: 2, loss: 0.083846, time elapsed: 47.5ms [1/125]
epoch: 2, loss: 0.082749, time elapsed: 45.1ms [51/125]
epoch: 2, loss: 0.081391, time elapsed: 46.2ms [101/125]
epoch: 3, loss: 0.081744, time elapsed: 47.2ms [1/125]
epoch: 3, loss: 0.080608, time elapsed: 45.8ms [51/125]
epoch: 3, loss: 0.082139, time elapsed: 45.1ms [101/125]
epoch: 4, loss: 0.080847, time elapsed: 47.6ms [1/125]
epoch: 4, loss: 0.083495, time elapsed: 46.0ms [51/125]
epoch: 4, loss: 0.083020, time elapsed: 45.3ms [101/125]
epoch: 5, loss: 0.079421, time elapsed: 76.9ms [1/125]
epoch: 5, loss: 0.062890, time elapsed: 44.6ms [51/125]
epoch: 5, loss: 0.018953, time elapsed: 45.2ms [101/125]
epoch: 6, loss: 0.012071, time elapsed: 49.6ms [1/125]
epoch: 6, loss: 0.007686, time elapsed: 45.5ms [51/125]
epoch: 6, loss: 0.006134, time elapsed: 73.7ms [101/125]
epoch: 7, loss: 0.005750, time elapsed: 47.2ms [1/125]
epoch: 7, loss: 0.004908, time elapsed: 45.7ms [51/125]
epoch: 7, loss: 0.003643, time elapsed: 45.6ms [101/125]
epoch: 8, loss: 0.002799, time elapsed: 48.2ms [1/125]
epoch: 8, loss: 0.002110, time elapsed: 45.5ms [51/125]
epoch: 8, loss: 0.001503, time elapsed: 46.6ms [101/125]
epoch: 9, loss: 0.001195, time elapsed: 48.0ms [1/125]
epoch: 9, loss: 0.000700, time elapsed: 45.5ms [51/125]
epoch: 9, loss: 0.000478, time elapsed: 47.1ms [101/125]
epoch: 10, loss: 0.000392, time elapsed: 71.8ms [1/125]
epoch: 10, loss: 0.000315, time elapsed: 45.8ms [51/125]
epoch: 10, loss: 0.000236, time elapsed: 50.4ms [101/125]
epoch: 11, loss: 0.000218, time elapsed: 48.4ms [1/125]
epoch: 11, loss: 0.000184, time elapsed: 46.4ms [51/125]
epoch: 11, loss: 0.000171, time elapsed: 54.9ms [101/125]
epoch: 12, loss: 0.000145, time elapsed: 47.7ms [1/125]
epoch: 12, loss: 0.000144, time elapsed: 46.9ms [51/125]
epoch: 12, loss: 0.000126, time elapsed: 60.5ms [101/125]
epoch: 13, loss: 0.000111, time elapsed: 48.6ms [1/125]
epoch: 13, loss: 0.000109, time elapsed: 46.7ms [51/125]
epoch: 13, loss: 0.000090, time elapsed: 45.3ms [101/125]
epoch: 14, loss: 0.000094, time elapsed: 48.0ms [1/125]
epoch: 14, loss: 0.000079, time elapsed: 46.1ms [51/125]
epoch: 14, loss: 0.000070, time elapsed: 47.6ms [101/125]
epoch: 15, loss: 0.000193, time elapsed: 53.1ms [1/125]
epoch: 15, loss: 0.000066, time elapsed: 47.7ms [51/125]
epoch: 15, loss: 0.000118, time elapsed: 49.3ms [101/125]
epoch: 16, loss: 0.000074, time elapsed: 48.7ms [1/125]
epoch: 16, loss: 0.000054, time elapsed: 85.8ms [51/125]
epoch: 16, loss: 0.000065, time elapsed: 97.4ms [101/125]
epoch: 17, loss: 0.000050, time elapsed: 101.0ms [1/125]
epoch: 17, loss: 0.000056, time elapsed: 86.3ms [51/125]
epoch: 17, loss: 0.000045, time elapsed: 46.8ms [101/125]
epoch: 18, loss: 0.000043, time elapsed: 107.0ms [1/125]
epoch: 18, loss: 0.000043, time elapsed: 46.4ms [51/125]
epoch: 18, loss: 0.000050, time elapsed: 45.9ms [101/125]
epoch: 19, loss: 0.000038, time elapsed: 95.2ms [1/125]
epoch: 19, loss: 0.000051, time elapsed: 76.3ms [51/125]
epoch: 19, loss: 0.000044, time elapsed: 44.7ms [101/125]
End-to-End total time: 148.45410752296448 s
[8]:
from src import visual, calculate_l2_error
模型预测可视化
[9]:
visual(model, config, resolution=config["visual_resolution"])
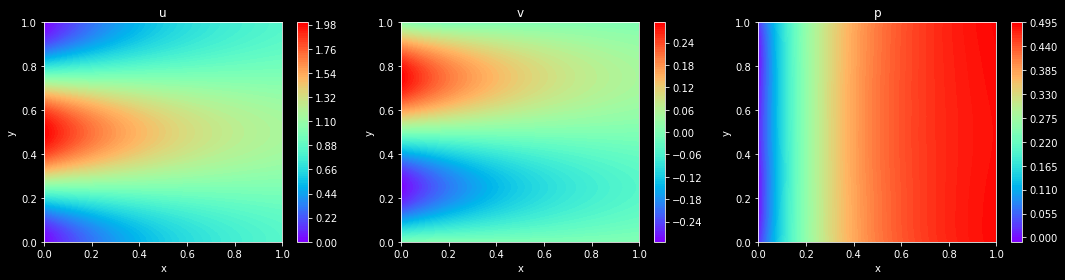
模型评估
[12]:
n_samps = 10000 # Number of test samples
ds_test = create_dataset(config, n_samps)
calculate_l2_error(problem, model, ds_test)
u: 1 - exp(-1.81009812001397*x)*cos(2*pi*y)
Item numbers of current derivative formula nodes: 2
v: -0.905049060006983*exp(-1.81009812001397*x)*sin(2*pi*y)/pi
Item numbers of current derivative formula nodes: 1
p: 0.5 - 0.5*exp(-3.62019624002793*x)
Item numbers of current derivative formula nodes: 2
Relative L2 error on domain: 0.003131713718175888
Relative L2 error on boundary: 0.0069109550677239895