基于MindSpore Quantum的Shor算法

下载Notebook  下载样例代码  查看源文件

Shor算法简介

Shor算法在量子计算机上分解整数\(N\)的时间复杂度为\(logN\)的多项式，几乎是对已知最有效的经典因数分解算法的\(e\)指数级加速，这种加速有可能在量子计算机上中断如RSA的现代加密机制。

Shor算法基本思路

Shor算法要解决的主要问题是：给定一个整数\(N\)，找出它的质因数。即对一个给定的较大数\(N\)在多项式时间内确定两个素因子 \(p1\)和\(p2\)满足\(p1\cdot p2=N\)。在介绍Shor算法步骤之前，先介绍一些数论知识。

因子分解涉及到数论里的一些知识，可以将因子分解问题归结为函数

\[f(x)=a^x \bmod N\]

对于\(a\)的周期查找（\(a\)和\(N\)互质，否则通过调用\(gcd(a,N)\)就可以马上得到一个因子）。由于函数\(f(x)\)存在周期\(r\)满足\(f(x)=f(x+r)\)。在这种情形下，就可得

\[a^x=a^{x+r} \bmod N\, \forall x\]

令\(x=0\)，得到\(a^r=1+qN\)，其中\(q\)为某一整数，即

\[a^r-1=(a^{r/2}-1)(a^{r/2}+1)=qN\]

这也表明对于\(N\)使用\(gcd\)就可以找到其因子。

因此，Shor算法的核心在于，将大数分解的问题转化为找周期的问题。由于量子计算可以利用叠加态进行并行计算，因此通过量子算法我们可以很快地找到函数\(f(x)\)的周期\(r\)（具体的原理和步骤请参考本文档中的周期查找算法）。总的来说，我们需要在量子线路中实现\(f(|x\rangle)=a^{|x\rangle} \bmod N\)的函数运算，可以构造一个酉矩阵\(U_{a,N}\)使得\(U_{a,N}|x\rangle |y\rangle \rightarrow |x\rangle |y \oplus f(x) \rangle\)，然后利用量子傅立叶变换我们就可以找到周期\(r\)满足\(a^r\equiv 1( \bmod N)\)。

下面以 \(N=15\)为例，介绍Shor算法在因子分解的步骤：

  1. 选择一个任意的数字，比如\(a=2(<15)\)

  2. 求最大公约数，\(gcd(a,N)=gcd(2,15)=1\)

  3. 找函数\(f(x)=a^x \bmod N\)的周期，使得\(f(x+r)=f(x)\)

  4. 通过量子电路图运算得到\(r=4\)

  5. 求最大公约数，\(\gcd(a^{r/2}+1,N)=\gcd(5,15)=5\)

  6. 求最大公约数，\(\gcd(a^{r/2}-1,N)=\gcd(3,15)=3\)

  7. \(N=15\)分解得到的质数结果为3和5，分解完成。

Shor算法的量子电路如下图所示：

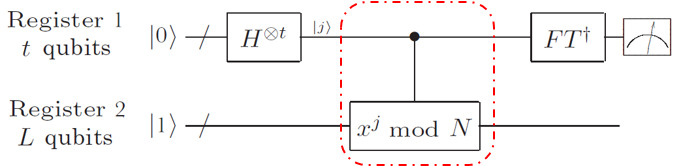
shor's algorithm circuit

通过MindSpore Quantum实现Shor算法

首先，导入需要用到的模块。

[1]:

#pylint: disable=W0611
import numpy as np
from fractions import Fraction
from mindquantum.core.gates import X, H, UnivMathGate, Measure
from mindquantum.core.circuit import Circuit, UN
from mindquantum.algorithm.library import qft
from mindquantum.simulator import Simulator

从Shor算法的基本思路我们可以看出，Shor算法最核心的部分就在于由量子计算机处理的周期查找算法，而周期查找算法中最困难的地方就是将态\(|x\rangle |y\rangle\)变为\(|x\rangle |y \oplus f(x) \rangle\)的算子\(U\)，这个算子的量子线路构造较为复杂，因此以下我们先通过经典计算机算出算子\(U\)并当作一个Oracle，以便本文档可以整体而直观地演示出Shor算法。

构造Oracle

Shor算法的核心量子部分是周期查找，其关键在于高效实现一个酉算子 \(U_{a,N}\)。这个算子作用在两个量子寄存器上（寄存器1存储指数 \(x\)，寄存器2存储辅助计算结果 \(y\)），并执行可逆的模幂运算。

具体来说，我们需要构建的酉算子 \(U_{a,N}\) 必须精确实现以下变换，对于所有可能的输入基态 \(|x\rangle|y\rangle\)：

\[U_{a,N} |x\rangle |y\rangle = |x\rangle |y \oplus (a^x \bmod N)\rangle\]

其中：

  • \(|x\rangle\) 是大小为 \(q\) 比特的寄存器，用于存储 \(0\) 到 \(Q-1\)（\(Q=2^q \ge N\)）的指数。

  • \(|y\rangle\) 也是大小为 \(q\) 比特的寄存器，用于存储中间结果。

  • \(a^x \bmod N\) 是经典的模幂计算结果。

  • \(\oplus\) 表示按位异或（XOR）操作。选择XOR是为了方便构建对应的酉矩阵（置换矩阵），并确保操作的可逆性。

虽然完整的 \(|y \oplus f(x)\rangle\) 变换需要更复杂的量子电路（如量子模加器和模乘器），但我们可以直接构建这个 \(2^{2q} \times 2^{2q}\) 的酉矩阵 \(U_{a,N}\)。该矩阵本质上是一个置换矩阵，它将每个输入基态 \(|x\rangle|y\rangle\) 唯一地映射到输出基态 \(|x\rangle|y \oplus (a^x \bmod N)\rangle\)。

实现步骤

  1. 确定比特数：

    • 目标寄存器 (寄存器2): 需要 \(q = \lceil \log_{2} N \rceil\) 个量子比特来存储 \(a^x \bmod N\) 的结果 (范围从 \(0\) 到 \(N-1\))。

    • 控制寄存器 (寄存器1): 存储指数 \(x\)。为了保证量子傅立叶变换能够以高概率给出周期 \(r\) 的相关信息，该寄存器中的量子比特数 \(t_q\) 应满足 \(2^{t_q} \ge N^2\)，即 \(t_q \ge 2 \log_{2} N\)。因此，理论上通常选择 \(t_q = 2q\)。令 \(Q_{ctrl} = 2^{t_q}\) 为控制寄存器的状态空间大小。

    • 本教程的简化： 由于本教程主要用于演示，并且考虑到模拟大规模量子系统所需的资源，我们在实现中使用 \(t_q = q\) 个量子比特作为控制寄存器，即 \(Q_{ctrl} = 2^q\)。此时，总量子比特数为 \(n_{total} = q + t_q = 2q\)。虽然这种简化在 \(N=15, a=2\) 的示例中仍可得到正确结果，但对于更大的 \(N\)，使用 \(t_q = q\) 会显著降低找到正确周期 \(r\) 的概率，可能需要多次尝试或只得到 \(r\) 的因子，甚至失败。

    • 因此，在本教程的后续部分，当提到控制寄存器的比特数或其对应的状态数 \(Q\) 时，我们指的是简化后的 \(q\) 比特与 \(Q=2^q\)。

  2. 计算模幂值： 对所有 \(x \in [0, Q-1]\)，计算 \(f(x) = a^x \bmod N\)。

  3. 构建酉矩阵U： 创建一个 \(2^n \times 2^n\) 的矩阵，初始化为零矩阵。对于每一个可能的输入基态 \(|x\rangle|y\rangle\)（其中 \(x, y \in [0, Q-1]\)），计算其对应的输出基态 \(|x\rangle|y \oplus f(x)\rangle\)。

    • 输入态 \(|x\rangle|y\rangle\) 在计算基矢中的索引为 \(idx_{in} = (x \ll q) + y\)。（这里 << 表示按位左移）

    • 输出态 \(|x\rangle|y \oplus f(x)\rangle\) 在计算基矢中的索引为 \(idx_{out} = (x \ll q) + (y \oplus f(x))\) (这里使用 \(\oplus\) 表示按位XOR)。

    • 在酉矩阵 \(U\) 中，将位置 \((idx_{out}, idx_{in})\) 的元素设为1。这构建了一个置换矩阵，它是酉的。

  4. 创建 ``UnivMathGate``： 使用构建好的酉矩阵 \(U\) 来实例化一个 UnivMathGate。

以 N=15, a=2 为例

我们需要 \(q=4\) 个比特，因为 \(2^4 = 16 \ge 15\)。总比特数 \(n = 2q = 8\)。希尔伯特空间维度为 \(2^8 = 256\)。

我们可以得到\(x\)与\(f(x)\)：

[2]:

q = 4  # 比特数
N = 15
a = 2
x = []
f = []
for i in range(2**q):
    x.append(i)
    f.append(a**i % N)
print('x: ', x)
print('f(x): ', f)

x:  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
f(x):  [1, 2, 4, 8, 1, 2, 4, 8, 1, 2, 4, 8, 1, 2, 4, 8]

可以观察到，\(f(x)\)确实是一个周期函数。

接下来我们构建出模幂运算对应的酉矩阵门：

[3]:

def create_mod_exp_oracle(N, a, register1, register2):
    """
    构建模幂运算 U|x>|y> = |x>|y XOR (a^x mod N)> 的门。

    Args:
        N (int): 需要分解的数。
        a (int): Shor算法中选择的随机基数。
        register1 (list): 寄存器1的比特索引，寄存器所需的比特数 (2^q >= N)。
        register2 (list): 寄存器2的比特索引，寄存器所需的比特数 (2^q >= N)。

    Returns:
        UnivMathGate，模幂运算 U|x>|y> = |x>|y XOR (a^x mod N)> 对应的门。
    """
    q = len(register1)
    n_qubits = 2 * q
    dim = 2**n_qubits
    Q = 2**q
    U_matrix = np.zeros((dim, dim), dtype=complex)

    # 预计算 f(x) = a^x mod N
    fx_map = {}
    for x in range(Q):
        fx_map[x] = pow(a, x, N)

    # 构建置换矩阵
    for x in range(Q):       # 遍历寄存器1的状态 |x>
        fx = fx_map[x]
        for y in range(Q):   # 遍历寄存器2的状态 |y>
            idx_in = (x << q) + y         # |x>|y> 的索引
            idx_out = (x << q) + (y ^ fx) # |x>|y XOR f(x)> 的索引
            U_matrix[idx_out, idx_in] = 1

    # 验证酉性
    assert np.allclose(U_matrix @ U_matrix.conj().T, np.eye(dim))

    # 创建门
    oracle_gate = UnivMathGate(f'ModExp({a},{N})', U_matrix).on(register2 + register1)
    return oracle_gate

现在，通过create_mod_exp_oracle()函数构造的门就可以对寄存器1中的量子态\(|x\rangle\)进行模幂运算，并将得到的结果\(a^{|x\rangle} \bmod N\)存入寄存器2。

小端序约定与 Qubit 分配：

MindQuantum 采用小端序（little-endian）约定来表示量子态。在此约定下，qubit 的索引与其在表示数值时的比特位重要性相对应：索引最低的 qubit (索引 0) 代表数值的最低有效位 (Least Significant Bit, LSB)。因此，一个 N-qubit 的状态通常写作 \(|q_{N-1}...q_1q_0\rangle\)，其中 \(q_0\) 是 LSB。

为了使 MindQuantum 的小端序约定与前文中的 \(|x\rangle |y\rangle\) 等量子态写法自然对齐，我们进行如下 qubit 分配：

  • 寄存器1 (逻辑值 :math:`x`): Qubits \(q\) 到 \(2q-1\) (高位 qubits)。

  • 寄存器2 (逻辑值 :math:`y`): Qubits \(0\) 到 \(q-1\) (低位 qubits)。

这意味着，尽管 Shor 算法的线路示意图中寄存器 1 在寄存器 2 的上方，但在 MindQuantum 中画出的线路图将是寄存器 2 在 寄存器 1 的上方，并且量子门和量子测量的位置都需要进行相应调整。

这种分配方式确保了在 MindQuantum 的状态向量表示中，与逻辑值 \(y\) (对应数值的低位部分) 相关的 qubits 具有较低的索引，而与逻辑值 \(x\) (对应数值的高位部分) 相关的 qubits 具有较高的索引。这样做的好处是，整个量子态对应的状态向量索引能够直接映射为整数值 \(x \cdot 2^q + y\)，这简化了类似 UnivMathGate 等操作的矩阵构建过程。需要强调的是，这种基于索引的分配方式不改变 Oracle 的核心逻辑功能，即根据寄存器 1 的值 \(x\) 来修改寄存器 2 的值 \(y\)。

验证Oracle

我们可以通过将Oracle应用于一个具体的初态来验证它是否按预期工作。例如，我们计算 \(U |8\rangle |0\rangle\)。我们期望得到 \(|8\rangle |0 \oplus (2^8 \bmod{15})\rangle\)。

因为 \(2^8 = 256\)，且 \(256 \bmod{15} = 1\)，所以 \(0 \oplus 1 = 1\)。我们期望末态是 \(|8\rangle |1\rangle\)。

\(|8\rangle\) 对应的二进制是 1000。 \(|1\rangle\) 对应的二进制是 0001。 所以末态 \(|8\rangle|1\rangle\) 对应的二进制是 1000 0001。

[4]:

# pylint: disable=W0104
register1 = range(4, 8)
register2 = range(4)
circuit = Circuit(X.on(7))  # 创建线路，使输入态为|1000⟩|0000⟩，即x=8，|8⟩|0⟩
circuit += create_mod_exp_oracle(15, 2, list(register1), list(register2))  # 作用oracle算子
circuit.svg() #打印线路

[4]:
../_images/case_library_shor_algorithm_7_0.svg
[5]:

print(circuit.get_qs('mqvector', ket=True))  # 打印末态

1¦10000001⟩

寄存器1中结果为1000，寄存器2中结果为0001，先前我们已经算出了\(f(8)=2^8 \bmod 15=1\)，因此输出结果正确。

接下来我们需要实现周期查找算法。

周期查找算法

  1. 在寄存器1中我们需要\(q>log_2 N\)个比特来记录自变量\(x \in [0,N-1]\)的二进制数，寄存器2中同样需要\(q\)个比特来记录\(f(x)=a^x \bmod N, x \in [0,N-1]\)的二进制数。此时寄存器1和寄存器2分别能记录\([0,Q-1]\)的整数,其中\(Q=2^q>N\)。

  2. 对寄存器1中的所有比特作用 Hadamard 门，此时寄存器1中的比特处于\([0,Q-1]\)中所有整数的均匀叠加态

    \[|\psi\rangle=\frac{1}{\sqrt{Q}}\sum_{x=0}^{Q-1}|x\rangle\]

  3. 对寄存器1存储的态\(|\psi\rangle\)做函数运算\(a^{|\psi\rangle} \bmod N\)，并将结果存入寄存器2，此步骤由先前构造的U_operator完成。由于直接对叠加态\(|\psi\rangle\)进行运算，此步骤只需一步完成，体现了量子计算的优势————并行计算。此时线路中存储的态是纠缠态，可以表示为

    \[\sum_{x=0}^{Q-1}|x\rangle|f(x)\rangle=\sum_{i=0}^{r-1}(|i\rangle+|i+r\rangle+|i+2r\rangle+...) |f(i)\rangle\]

  4. 对寄存器1做傅立叶逆变换，此变换使用一个\(Q\)次单位根\(\omega^{2\pi i/Q}\)，会将任意给定态\(|x\rangle\)的振幅平均分布在\(Q\)个\(|y\rangle\)态上。而如步骤3中显示的，寄存器1中\(|i\rangle\)与\(|i+r\rangle\)等态均与寄存器2中同一个态\(|f(i)\rangle\)相纠缠，因此会发生量子干涉，最终使得当单位矢量\(\omega^{2\pi iry/Q}\)越接近1（指向正实数轴）时，测量得到态\(|y\rangle\)的概率越大。换句话说，我们测得的态\(|y\rangle\)，有很大概率使得\(\frac{ry}{Q}\)接近某一整数\(c\)。更详尽的数学描述可以参考链接：https://zh.wikipedia.org/wiki/秀爾演算法 中的“量子部分：周期查找子程序”。

  5. 测量寄存器1，得到二进制串。将二进制数转化为十进制数\(y\)，此时\(\frac{y}{Q}\sim\frac{c}{r}\)，其中\(c\)是未知整数。通过连分数分解法计算\(\frac{y}{Q}\)逼近的不可约分数（分母不大于\(N\)），取其分母即得到周期\(r\)。但是，在分母小于\(N\)的不可约分数中可能存在比\(\frac{c}{r}\)更逼近\(\frac{y}{Q}\)的分数，或是\(c\)与\(r\)存在公因数，则得到的\(r\)会是真正函数周期的因数，此时计算失败，重新计算。

举例：还是用\(N=15, a=2\)的例子，在构造Oracle中我们把每一个\(f(x)\)都算了出来，从中可以直接看出函数周期为4。现在我们可以搭建对应的周期查找线路，并进行100次模拟，看看会得到哪些结果。

[6]:

# pylint: disable=W0104
circuit = Circuit()  # 创建量子线路
register1 = range(4, 8)  # 设置后4个比特为寄存器1
register2 = range(4)  # 设置前4个比特为寄存器2

circuit += UN(H, register1)  # 对寄存器1中的所有比特作用H门

# 对寄存器1做模乘运算，并将结果存入寄存器2，该操作由一个大的U门完成
circuit += create_mod_exp_oracle(15, 2, list(register1), list(register2))

circuit += qft(register1[::-1]).hermitian()  # 对寄存器1做傅立叶逆变换，须注意傅立叶变换作用的比特顺序，在这里需要反序
circuit += UN(Measure(), register1)  # 测量寄存器1

circuit.svg()  # 画出线路图

[6]:
../_images/case_library_shor_algorithm_12_0.svg

从线路图我们可以很直观地看到，整个周期查找线路由四部分组成：

  1. 产生叠加态

  2. \(rightarrow\)函数运算

  3. \(rightarrow\)傅立叶逆变换

  4. \(rightarrow\)测量

接下来运行该线路100次，观察测量结果。

[7]:

# pylint: disable=W0104
sim = Simulator('mqvector', circuit.n_qubits)  # 创建量子线路模拟器

# 模拟线路100次，打印测量结果，随机种子seed设为100内的随机整数
result = sim.sampling(circuit, shots=100, seed=np.random.randint(100))

result.svg()

[7]:
../_images/case_library_shor_algorithm_14_0.svg

从统计结果可以看出，最后寄存器1中只可能测出4个态，分别是\(y=[0,4,8,12]\)，这是由于\(\omega^{2\pi iry/Q}, (Q=16)\)当\(y\)取这四个值时恰好为1，而其他的态由于量子干涉导致概率幅抵消为零。把测量结果代入\(\frac{y}{Q}\sim\frac{c}{r}\)，可以看出该式确实成立，我们有约50%的概率得到正确的周期\(r\)，但有约25%概率得到\(r\)的因数，还有25%概率得到0态，后两种情况需要重新计算。

接下来构造的是通用的周期查找算法。

[8]:

def period_finder(N, a, q):
    circuit = Circuit()  # 创建量子线路
    register1 = range(q, 2 * q)  # 设置后q个比特为寄存器1
    register2 = range(q)  # 设置前q个比特为寄存器2

    circuit += UN(H, register1)  # 对寄存器1中的所有比特作用H门

    # 对寄存器1做模乘运算，并将结果存入寄存器2，该操作由一个大的U门完成
    circuit += create_mod_exp_oracle(N, a, list(register1), list(register2))

    circuit += qft(register1[::-1]).hermitian()  # 对寄存器1做傅立叶逆变换，须注意傅立叶变换作用的比特顺序，在这里需要反序
    circuit += UN(Measure(), register1)  # 测量寄存器1

    sim = Simulator('mqvector', circuit.n_qubits)  # 创建量子线路模拟器

    # 模拟线路，收集测量结果，随机种子seed设为100内的随机整数
    result = sim.sampling(circuit, seed=np.random.randint(100), shots=1)

    # result.data是一个字典，key是测量结果，value是出现频数，我们只做了一次采样，因此只有一个key，value必定为1
    result = list(result.data.keys())[0]  # 将key取出
    result = int(result, 2)  # 将结果从二进制转化为十进制

    # 通过连分数分解法计算result/2**q逼近的不可约分数，分母不能大于N
    eigenphase = float(result / 2**q)
    f = Fraction.from_float(eigenphase).limit_denominator(N)
    r = f.denominator  # 取f的分母，得到周期r

    # r有可能是周期的因数，因此需要验证，当且仅当r是函数周期本身时返回r，否则返回None
    if pow(a, r, N) == 1:
        return r
    return None

经典计算机部分

经典计算机部分负责将因数分解问题转化成寻找函数周期的问题，具体步骤如下：

  1. 随机取一个小于\(N\)的整数\(a\)，用gcd算法验证\(a\)与\(N\)是否互质，若\(a\)与\(N\)存在公因数，则直接得到\(N\)的一个因数，输出结果。

  2. 计算需要\(q\)个比特来存储\(N\)的二进制数。

  3. 用周期查找算法得到函数\(f(x)=a^x \bmod N\)的周期\(r\)。

  4. 判断\(r\)是否为偶数，若不是则回到第一步。

  5. 计算\(a^{r/2}+1\)和\(a^{r/2}-1\)，它们当中必有其一与\(N\)存在非1公因数。但是，\(a^{r/2}+1\)有可能可以整除\(N\)，因此最后输出结果仍有可能是\(N\)本身。

[9]:

#pylint: disable=C0121,R1705
def shor(N):
    while True:
        a = np.random.randint(N - 2) + 2  # 获得区间[2,N-1]内的随机整数a
        b = np.gcd(a, N)  # 得到a与N的最大公因数b
        if b != 1:
            return b, int(N / b)  # 如果b不等于1，则b是N的质因数，返回分解结果

        # 获得足够表示N的二进制的比特数q
        q = 0
        while True:
            Q = 2**q
            if Q >= N:
                break
            q += 1

        r = period_finder(N, a, q)  # 使用周期查找算法得到r

        # 判断r是否为偶数,若是则跳出循环，若不是则重新选择随机整数a
        if r != None and r % 2 == 0:
            break

    # 计算a**(r/2)+1和a**(r/2)-1，并验证它们是否与N有公约数，若有则输出结果
    c = np.gcd(a**(int(r / 2)) + 1, N)
    d = np.gcd(a**(int(r / 2)) - 1, N)
    if c != 1 and N % c == 0:
        return c, int(N / c)
    else:
        return d, int(N / d)

需要注意的是，由于我们直接将oracle构造为了一个巨大的酉矩阵门，导致了模拟耗时的大幅增加，因此对于\(N>55\)的情况，可能需要较长的时间才能得到结果。并且由于前文提到寄存器 1 比特数量的简化，N更大的时候找到正确周期的概率会比较小。

最后让我们试着用写好的Shor算法分解\(N=35\)。

[10]:

N = 35
print("Factoring N = p * q =", N)

p, q = shor(N)
print("p =", p)
print("q =", q)

Factoring N = p * q = 35
p = 5
q = 7

从运行结果可以看到，我们成功的分解出35的两个质因数：5和7。

至此，我们成功的使用MindSpore Quantum实现了Shor算法。

[11]:

from mindquantum.utils.show_info import InfoTable

InfoTable('mindquantum', 'scipy', 'numpy')

[11]:
Software Version
mindquantum0.10.0
scipy1.15.2
numpy1.26.4
System Info
Python3.10.16
OSDarwin arm64
Memory17.18 GB
CPU Max Thread10
DateFri May 16 19:23:31 2025