Document feedback

Question document fragment

When a question document fragment contains a formula, it is displayed as a space.

Submission type

issue

It's a little complicated...

I'd like to ask someone.

Please select the submission type

Problem type

Specifications and Common Mistakes

- Specifications and Common Mistakes:

- Misspellings or punctuation mistakes,incorrect formulas, abnormal display.

- Incorrect links, empty cells, or wrong formats.

- Chinese characters in English context.

- Minor inconsistencies between the UI and descriptions.

- Low writing fluency that does not affect understanding.

- Incorrect version numbers, including software package names and version numbers on the UI.

Usability

- Usability:

- Incorrect or missing key steps.

- Missing main function descriptions, keyword explanation, necessary prerequisites, or precautions.

- Ambiguous descriptions, unclear reference, or contradictory context.

- Unclear logic, such as missing classifications, items, and steps.

Correctness

- Correctness:

- Technical principles, function descriptions, supported platforms, parameter types, or exceptions inconsistent with that of software implementation.

- Incorrect schematic or architecture diagrams.

- Incorrect commands or command parameters.

- Incorrect code.

- Commands inconsistent with the functions.

- Wrong screenshots.

- Sample code running error, or running results inconsistent with the expectation.

Risk Warnings

- Risk Warnings:

- Lack of risk warnings for operations that may damage the system or important data.

Content Compliance

- Content Compliance:

- Contents that may violate applicable laws and regulations or geo-cultural context-sensitive words and expressions.

- Copyright infringement.

Please select the type of question

Problem description

Describe the bug so that we can quickly locate the problem.

Submit

Document feedback

1D Sod Tube

  

This notebook requires MindSpore version >= 2.0.0 to support new APIs including: mindspore.jit, mindspore.jit_class.

The shock tube problem is a common test for the accuracy of computational fluid codes, like Riemann solvers. The test consists of a one-dimensional Riemann problem with left and right states of an ideal gas.

Problem Description

The definition of the Sod tube problem is:

$$\begin{array}{r}\frac{\partial }{\partial t}\left(\begin{array}{c}\rho \\ \rho u\\ E\end{array}\right)+\frac{\partial }{\partial x}\left(\begin{array}{c}\rho u\\ \rho u^2+p\\ u(E+p)\end{array}\right)=0\end{array}$$

$$E=\frac{p}{\gamma -1}+\frac{1}{2}\rho u^2$$

where $\gamma =1.4$ for ideal gas. The initial condition is

$$\begin{array}{r}{\left(\begin{array}{c}\rho \\ u\\ p\end{array}\right)}_{x<0.5}=\left(\begin{array}{c}1.0\\ 0.0\\ 1.0\end{array}\right),{\left(\begin{array}{c}\rho \\ u\\ p\end{array}\right)}_{x>0.5}=\left(\begin{array}{c}0.125\\ 0.0\\ 0.1\end{array}\right)\end{array}$$

The Neumann boundary condition is applied on both side of the tube.

The following src pacakage can be downloaded in src.

import mindspore as ms
from mindflow import load_yaml_config, vis_1d
from mindflow import cfd
from mindflow.cfd.runtime import RunTime
from mindflow.cfd.simulator import Simulator

from src.ic import sod_ic_1d

ms.set_context(device_target="GPU", device_id=3)

Define Simulator and RunTime

The mesh, material, runtime, boundary conditions and numerical methods are defined in numeric.yaml.

config = load_yaml_config('numeric.yaml')
simulator = Simulator(config)
runtime = RunTime(config['runtime'], simulator.mesh_info, simulator.material)

Initial Condition

Initial condition is determined according to mesh coordinates.

mesh_x, _, _ = simulator.mesh_info.mesh_xyz()
pri_var = sod_ic_1d(mesh_x)
con_var = cfd.cal_con_var(pri_var, simulator.material)

Run Simulation

Run CFD simulation with time marching.

while runtime.time_loop(pri_var):
    pri_var = cfd.cal_pri_var(con_var, simulator.material)
    runtime.compute_timestep(pri_var)
    con_var = simulator.integration_step(con_var, runtime.timestep)
    runtime.advance()

current time = 0.000000, time step = 0.007606
current time = 0.007606, time step = 0.005488
current time = 0.013094, time step = 0.004744
current time = 0.017838, time step = 0.004501
current time = 0.022339, time step = 0.004338
current time = 0.026678, time step = 0.004293
current time = 0.030971, time step = 0.004268
current time = 0.035239, time step = 0.004198
current time = 0.039436, time step = 0.004157
current time = 0.043593, time step = 0.004150
current time = 0.047742, time step = 0.004075
current time = 0.051818, time step = 0.004087
current time = 0.055905, time step = 0.004056
current time = 0.059962, time step = 0.004031
current time = 0.063993, time step = 0.004021
current time = 0.068014, time step = 0.004048
current time = 0.072062, time step = 0.004039
current time = 0.076101, time step = 0.004016
current time = 0.080117, time step = 0.004049
current time = 0.084166, time step = 0.004053
current time = 0.088218, time step = 0.004045
current time = 0.092264, time step = 0.004053
current time = 0.096317, time step = 0.004062
current time = 0.100378, time step = 0.004065
current time = 0.104443, time step = 0.004068
current time = 0.108511, time step = 0.004072
current time = 0.112583, time step = 0.004075
current time = 0.116658, time step = 0.004077
current time = 0.120735, time step = 0.004080
current time = 0.124815, time step = 0.004081
...
current time = 0.186054, time step = 0.004084
current time = 0.190138, time step = 0.004084
current time = 0.194222, time step = 0.004084
current time = 0.198306, time step = 0.004085

Post Processing

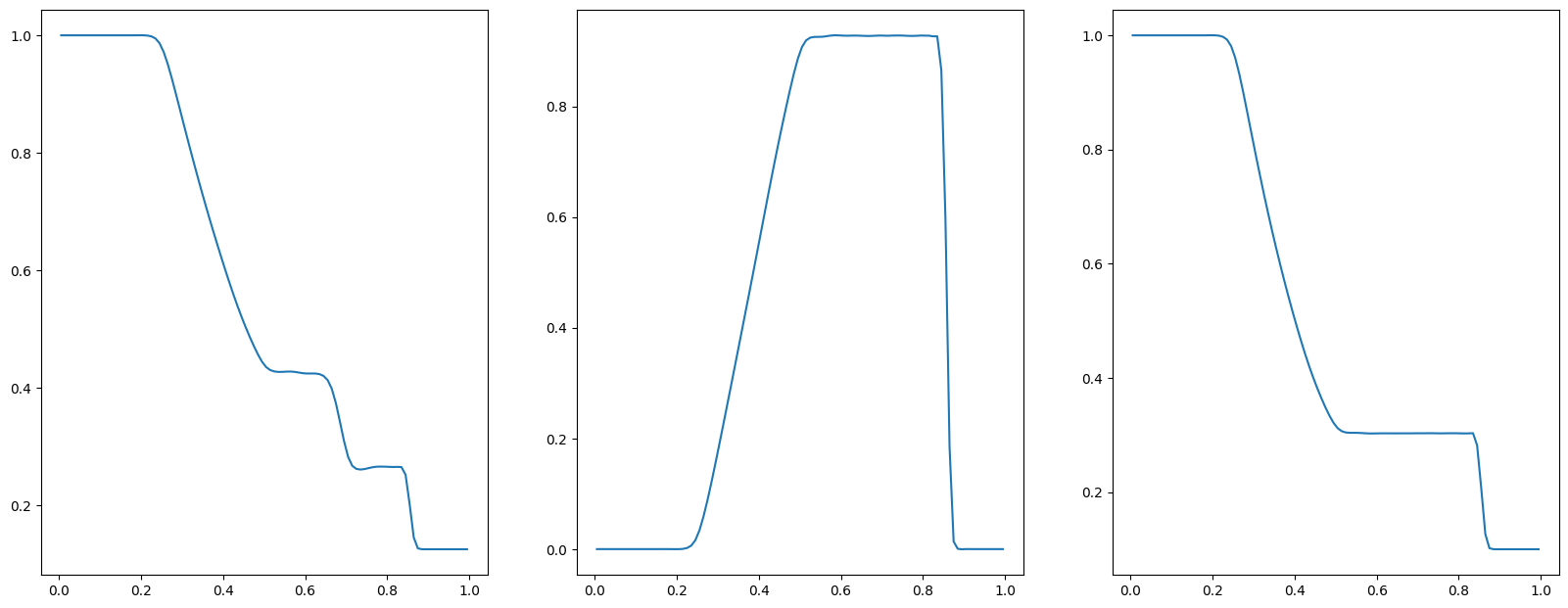
You can view the density, pressure and velocity.

pri_var = cfd.cal_pri_var(con_var, simulator.material)
vis_1d(pri_var, 'sod.jpg')