量子近似优化算法
概述
量子近似优化算法(Quantum Approximate Optimization Algorithm,QAOA)是利用量子计算机来近似解决组合优化问题的量子算法,最早由Farhi等人于2014年提出。在本文档里,我们将利用QAOA算法来解决最大割问题(Max-Cut),来熟悉MindQuantum中量子线路的搭建和训练。
本文档适用于CPU环境。 你可以在这里找到完整的可运行的样例代码:https://gitee.com/mindspore/mindquantum/blob/r0.6/tutorials/source/quantum_approximate_optimization_algorithm.py。
环境准备
本文档所需要的额外库:
networkx
networkx是创建、操作和研究复杂网络的结构、动态和功能库。可通过如下代码来进行安装。
pip3 install networkx
Max-Cut问题描述
Max-Cut问题是图论中的一个NP-complete问题,它需要将一个图中的顶点分成两部分,并使得两部分被切割的边最多。如下图(a),一个图由五个顶点构成,相互连接的边为(0, 1), (0, 2), (1, 2), (2, 3), (3, 4), (0, 4)。为了使得被切割的边最多,我们尝试通过(b)图的分割,将1、2、4分为一组,0、3分成另一组,因此可得到被切割的边有5条。后面我们将用穷举法验证这个解是否正确。当图中顶点较少时,我们可以在较短时间内通过穷举法找到最大的切割边数,但当图中顶点增多时,我们很难找到有效的经典算法来解决Max-Cut问题,因为这类NP-complete问题很有可能不存在多项式时间算法。但尽管精确解不容易得到,我们却可以想办法在多项式时间内找到问题的一个近似解,这就是近似优化算法。下面,我们介绍怎么将Max-Cut问题转化为一个哈密顿量的基态能量求解问题。

Max-Cut问题量子化
这里我们将图中的每个顶点赋予一个量子比特,当顶点被分到左边时,我们将该顶点上的量子比特设置为\(\left|0\right>\)态,同理,右边为\(\left|1\right>\)态,当两个顶点被分到不同的集合中时,这两个顶点上的比特将处于不同的量子态。例如对于第0个顶点和第1个顶点,当其连线被切割时,两个顶点上的比特对应的量子态可以表示为\(|01\rangle\)(顶点1:左,顶点0:右)或\(|10\rangle\)(顶点1:右,顶点0:左);若它们被分到同一边,则对应量子态为\(|00\rangle\)或\(|11\rangle\)。因此我们只要找到一个哈密顿量\(H\)使得:当有连线的两个顶点处于不同量子态时,哈密顿量的期望值为-1,即
而当有连线的顶点处于相同量子态时,哈密顿量的期望值为0,即
随后只要使哈密顿量的期望值最小化,就可以找到最大切割边数,以及此时对应的分组情况。之所以将不同量子态时的期望值设为-1,是因为在量子神经网络的训练中,Ansatz中的参数的梯度会一直下降,同时测量值也会一直减少,该训练方法就是以找到最小值为目标,这里我们用它来寻找哈密顿量的基态能量。此时,我们选择哈密顿量\(H=(Z_1Z_0-1)/2\),这里\(Z\)为泡利\(Z\)算符。此时有:
因此当顶点被分到不同集合时:
而当顶点被分到同一集合中时,不难验证此时:
因此,我们只要对图中的每条边写出上述哈密顿量,然后将所有边求和,即可写出图对应的哈密顿量\(H\),利用量子计算机求得\(H\)的基态能量与基态,我们就可以得到该图的Max-Cut切割方案与最大切割边数。我们记所有边的集合为\(C\),所有边条数为\(c\),则哈密顿量可写为:
导入相关依赖
[1]:
from mindquantum.core import Circuit, Hamiltonian, UN, H, ZZ, RX, QubitOperator
from mindquantum.framework import MQAnsatzOnlyLayer
from mindquantum.simulator import Simulator
import networkx as nx
import mindspore.nn as nn
搭建所需求解的图
通过add_path可在图中添加边。最后画出图的结构。
[2]:
g = nx.Graph()
nx.add_path(g, [0, 1])
nx.add_path(g, [1, 2])
nx.add_path(g, [2, 3])
nx.add_path(g, [3, 4])
nx.add_path(g, [0, 4])
nx.add_path(g, [0, 2])
nx.draw(g, with_labels=True, font_weight='bold')
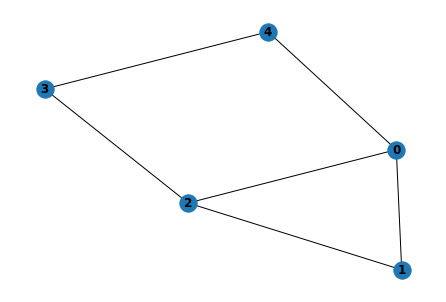
如上图,我们得到一个由5个节点和6条边构成的图结构。
接下来我们用穷举法来看看所有情况的切割边数。
[3]:
for i in g.nodes:
print('one size:', [i], 'cut=', nx.cut_size(g, [i])) # 一组1个节点、另一组4个节点的所有情况
for j in range(i):
print('one size:', [i, j], 'cut=', nx.cut_size(g, [i, j])) # 一组2个节点、另一组3个节点的所有情况
one size: [0] cut= 3
one size: [1] cut= 2
one size: [1, 0] cut= 3
one size: [2] cut= 3
one size: [2, 0] cut= 4
one size: [2, 1] cut= 3
one size: [3] cut= 2
one size: [3, 0] cut= 5
one size: [3, 1] cut= 4
one size: [3, 2] cut= 3
one size: [4] cut= 2
one size: [4, 0] cut= 3
one size: [4, 1] cut= 4
one size: [4, 2] cut= 5
one size: [4, 3] cut= 2
从以上结果可以看出,穷举法得到的最大切割边数为5,如果对节点分组的左右进行区分,则一共有4种分组方法可以使切割边数最大,即该问题有4个简并解。
QAOA算法整体流程
搭建QAOA量子线路,其中ansatz线路包含可以训练的参数
初始化线路中的参数
运行该量子线路,得到量子态\(|\psi\rangle\)
计算目标哈密顿量\(H_C\)的期望值\(\langle\psi|H_C|\psi\rangle\)
根据第4步的结果,使用Adam优化器优化线路中参数
重复3-5步,直到第4步结果基本不再变化
根据第4步的结果,算出目标问题的近似解
在该流程中,第2-6步都可以由MindSpore和MindQuantum中现成的包和函数来实现,因此我们将重点关注第1步——量子线路的搭建。

搭建QAOA量子线路
先前提到,我们需要将问题对应的哈密顿量
最小化来找到问题的解,也就是说我们要找到该哈密顿量的基态。对此我们可以采用量子绝热演化的方法,使系统先处于某一简单哈密顿量\(H_B\)的基态上,然后使简单的哈密顿量\(H_B\)绝热地、缓慢地演化至某一复杂的哈密顿量\(H_C\),根据绝热定理,系统将始终保持在哈密顿量的基态上,最终达到复杂哈密顿量\(H_C\)的基态。
我们将要搭建的量子线路就是采用以上思路,选取初始简单哈密顿量为
并将量子线路制备到\(H_B\)的基态\(|s\rangle=|+\rangle^{\otimes n}\),这里通过对所有量子比特作用Hadamard门即可实现。然后连接ansatz含参线路,通过不断地优化其中参数可以使得ansatz线路越来越接近真实绝热演化的效果,最终得到的量子线路可以视为模拟近似了一个真实的绝热演化过程。
ansatz线路
在量子绝热演化中,首先选取初始哈密顿量
并使系统处于\(H_B\)的基态\(|s\rangle=|+\rangle^{\otimes n}\)。然后缓慢地作用如下含时哈密顿量
注意到当\(t=T\)时,\(H(T)=H_C\)。当选取的\(T\)足够大时(满足绝热条件),系统将始终处于\(H(t)\)的瞬时基态上,此时系统的量子态将从初始哈密顿量\(H_B\)的基态\(|\psi (0)\rangle\)绝热地演化到目标哈密顿量\(H_C\)的基态\(|\psi (T)\rangle\)上,即
也就是说,ansatz线路需要模拟的就是\(\mathcal{T}e^{-i\int^{T}_{0} H(t)dt}\)这一演化过程。接下来我们将对这个式子进行一些近似和化简,使其变为可以在量子线路中实现的形式。
考虑如下trotter公式
略去\(O(\Delta t^2)\)项,得到
令\(\beta_l=(1-t_l/T)\Delta t\),\(\gamma_l=t_l\Delta t/T\),并取\(N\)为一个有限大的整数,即得到QAOA的ansatz
因此我们需要搭建的ansatz线路由\(U_C(\gamma)\)和\(U_B(\beta)\)这两个酉变换交替构成,其中\(U_C(\gamma)=e^{-i\gamma \sum_{\langle i,j\rangle}Z_i Z_j}\)可以由ZZ门实现,\(U_B(\beta)=e^{-i\beta \sum_i X_i}\)则相当于在每个量子比特上作用一个RX旋转门,\(\gamma\)和\(\beta\)是可训练的参数。
搭建\(U_C(\gamma)\)对应的量子线路:
[4]:
def build_hc(g, para):
hc = Circuit() # 创建量子线路
for i in g.edges:
hc += ZZ(para).on(i) # 对图中的每条边作用ZZ门
hc.barrier() # 添加Barrier以方便展示线路
return hc
线路展示:
[5]:
# pylint: disable=W0104
circuit = build_hc(g, 'gamma')
circuit.svg()
[5]:
搭建\(U_B(\beta)\)对应的量子线路:
[6]:
def build_hb(g, para):
hb = Circuit() # 创建量子线路
for i in g.nodes:
hb += RX(para).on(i) # 对每个节点作用RX门
hb.barrier() # 添加Barrier以方便展示线路
return hb
线路展示:
[7]:
# pylint: disable=W0104
circuit = build_hb(g, 'beta')
circuit.svg()
[7]:
实现了一层酉变换\(U_B(\beta) U_C(\gamma)\)的ansatz线路如下所示:
[8]:
# pylint: disable=W0104
circuit = build_hc(g, 'gamma') + build_hb(g, 'beta')
circuit.svg()
[8]:
为了使得最后优化的结果足够准确,我们需要将量子线路重复多次,因此我们通过如下函数搭建多层的训练网络:
[9]:
def build_ansatz(g, p): # g是max-cut问题的图,p是ansatz线路的层数
circ = Circuit() # 创建量子线路
for i in range(p):
circ += build_hc(g, f'g{i}') # 添加Uc对应的线路,参数记为g0、g1、g2...
circ += build_hb(g, f'b{i}') # 添加Ub对应的线路,参数记为b0、b1、b2...
return circ
构建图对应的哈密顿量\(H_C=\sum_{(i,j)\in C}(Z_iZ_j-1)/2\)(忽略常数项和系数):
[10]:
def build_ham(g):
ham = QubitOperator()
for i in g.edges:
ham += QubitOperator(f'Z{i[0]} Z{i[1]}') # 生成哈密顿量Hc
return ham
生成完整的量子线路和图所对应的哈密顿量
这里我们选择p = 4,表示选用4层的QAOA量子线路,ansatz是求解该问题的量子线路,init_state_circ是将量子态制备到均匀叠加态(\(H_B\)的基态)上的量子线路。
[11]:
# pylint: disable=W0104
p = 4
ham = Hamiltonian(build_ham(g)) # 生成哈密顿量
init_state_circ = UN(H, g.nodes) # 生成均匀叠加态,即对所有量子比特作用H门
ansatz = build_ansatz(g, p) # 生成ansatz线路
circ = init_state_circ + ansatz # 将初始化线路与ansatz线路组合成一个线路
circ.svg()
[11]:
搭建待训练量子神经网络
由于该问题不需要编码层量子线路,我们这里使用MQAnsatzOnlyLayer作为待训练的量子神经网络,并采用Adam优化器。
[12]:
import mindspore as ms
ms.context.set_context(mode=ms.context.PYNATIVE_MODE, device_target="CPU")
sim = Simulator('projectq', circ.n_qubits) # 创建模拟器,backend使用‘projectq’,能模拟5个比特('circ'线路中包含的比特数)
grad_ops = sim.get_expectation_with_grad(ham, circ) # 获取计算变分量子线路的期望值和梯度的算子
net = MQAnsatzOnlyLayer(grad_ops) # 生成待训练的神经网络
opti = nn.Adam(net.trainable_params(), learning_rate=0.05) # 设置针对网络中所有可训练参数、学习率为0.05的Adam优化器
train_net = nn.TrainOneStepCell(net, opti) # 对神经网络进行一步训练
训练并展示结果
[13]:
for i in range(200):
cut = (len(g.edges) - train_net()) / 2 # 将神经网络训练一步并计算得到的结果(切割边数)。注意:每当'train_net()'运行一次,神经网络就训练了一步
if i%10 == 0:
print("train step:", i, ", cut:", cut) # 每训练10步,打印当前训练步数和当前得到的切割边数
train step: 0 , cut: [3.0001478]
train step: 10 , cut: [4.1718774]
train step: 20 , cut: [4.6871986]
train step: 30 , cut: [4.7258005]
train step: 40 , cut: [4.804503]
train step: 50 , cut: [4.8477592]
train step: 60 , cut: [4.8705964]
train step: 70 , cut: [4.9060946]
train step: 80 , cut: [4.933446]
train step: 90 , cut: [4.9356637]
train step: 100 , cut: [4.938308]
train step: 110 , cut: [4.9390197]
train step: 120 , cut: [4.939068]
train step: 130 , cut: [4.9392157]
train step: 140 , cut: [4.939249]
train step: 150 , cut: [4.939247]
train step: 160 , cut: [4.939255]
train step: 170 , cut: [4.939257]
train step: 180 , cut: [4.939257]
train step: 190 , cut: [4.939257]
根据上面的训练结果我们发现,该问题哈密顿量的基态能量对应的边切割数趋近于5。
最优参数
前面我们通过训练得到了量子线路中参数的最优值,下面,我们将最优参数提取出来并存储为字典类型,与之前线路中命名的参数一一对应。
[14]:
pr = dict(zip(ansatz.params_name, net.weight.asnumpy())) # 获取线路参数
print(pr)
{'g0': 0.22448167, 'b0': -1.1390871, 'g1': 0.45314747, 'b1': -0.94472605, 'g2': 0.5338268, 'b2': -0.67756957, 'g3': 0.58400834, 'b3': -0.38243017}
概率图
我们将最优参数代入量子线路,通过对量子线路进行1000次采样,画出最终量子态在计算基矢下的概率分布:
[15]:
# pylint: disable=W0104
circ.measure_all() # 为线路中所有比特添加测量门
sim.sampling(circ, pr=pr, shots=1000).svg() # 运行线路1000次并打印结果
[15]:
根据概率分布图我们发现,该Max-Cut问题具有四个简并解,每个解对应的概率大概为25%。
01001:编号为1、2、4的顶点在左边,编号为0、3的顶点在右边。10110:编号为0、3的顶点在左边,编号为1、2、4的顶点在右边。01011:编号为2、4的顶点在左边,编号为0、1、3的顶点在右边。10100:编号为0、1、3的顶点在左边,编号为2、4的顶点在右边。
可以发现,以上结果与先前通过穷举法得到的结果相符。
总结
这里我们通过量子近似优化算法来解决了Max-Cut问题,并得到了案例中的图对应的最大切割方案。
参考文献
[1] Edward Farhi, Jeffrey Goldstone, and Sam Gutmann. A Quantum Approximate Optimization Algorithm
