PDE-Net求解对流扩散方程
概述
PDE-Net是Zichao Long等人提出的一种前馈深度网络用于从数据中学习偏微分方程,同时实现了准确预测复杂系统的动力学特性和揭示潜在的PDE模型。PDE-Net的基本思想是通过学习卷积核(滤波器)来逼近微分算子,并应用神经网络或其他机器学习方法来拟合未知的非线性响应。数值实验表明,即使在噪声环境中,该模型也可以识别被观测的动力学方程,并预测相对较长时间的动态行为。更多信息可参考PDE-Net: Learning PDEs from Data.
本案例要求MindSpore版本 >= 2.0.0以调用如下接口: mindspore.jit, mindspore.jit_class, mindspore.data_sink。
问题描述
本案例求解可变参数的对流-扩散偏微分方程的反问题,并实现长期预测。
控制方程
在本研究中,对流扩散方程的形式为:
各项导数的系数分别为:
PDE-Net的模型结构
PDE-Net由多个\(\delta T\) Block串联构成,以实现长序列信息的预测,在每一个\(\delta T\) Block中,包含可训练参数的moment矩阵,该矩阵可根据映射关系转化为对应导数的卷积核,从而获取物理场的导数。将导数及其对应物理量经线性组合后,采用前向欧拉法,即可推导下一个时间步的信息。


技术路径
MindSpore Flow求解该问题的具体流程如下:
构建模型。
单步训练。
多步训练。
模型推理及可视化。
[1]:
import os
import time
import numpy as np
import mindspore
from mindspore.common import set_seed
from mindspore import nn, Tensor, ops, jit
from mindspore.train.serialization import load_param_into_net
下述src可以在applications/data_mechanism_fusion/variant_linear_coe_pde_net/src下载。
[2]:
from mindflow.cell import PDENet
from mindflow.utils import load_yaml_config
from mindflow.loss import get_loss_metric, RelativeRMSELoss
from mindflow.pde import UnsteadyFlowWithLoss
from src import init_model, create_dataset, calculate_lp_loss_error
from src import make_dir, scheduler, get_param_dic
from src import plot_coe, plot_extrapolation_error, get_label_coe, plot_test_error
所有配置参数可以在configuration file修改。
[3]:
set_seed(0)
np.random.seed(0)
mindspore.set_context(mode=mindspore.GRAPH_MODE, device_target="GPU", device_id=3)
[4]:
# load configuration yaml
config = load_yaml_config('pde_net.yaml')
构建模型
MindSpore Flow提供了PDENet接口可以直接建立PDENet模型,需指定网格的宽度、高度、数据深度、边界条件、拟合的最高阶数等信息。
[5]:
def init_model(config):
return PDENet(height=config["mesh_size"],
width=config["mesh_size"],
channels=config["channels"],
kernel_size=config["kernel_size"],
max_order=config["max_order"],
dx=2 * np.pi / config["mesh_size"],
dy=2 * np.pi / config["mesh_size"],
dt=config["dt"],
periodic=config["perodic_padding"],
enable_moment=config["enable_moment"],
if_fronzen=config["if_frozen"],
)
单步训练
由于每个\(\delta T\) Block的参数是共享的,因此模型根据\(\delta T\) Block的串联个数依次增加,逐一进行训练。其中,在step为1时,模型处于warm-up阶段,PDE-Net的moment为“frozen”状态,此时moment中的参数不参与训练。每新增一个\(\delta T\) Block,程序先进行数据生成和数据集的读取,初始化模型后,需载入前一个step训练的checkpoint,并定义优化器、模式、loss函数,并进行模型训练,在训练中模型会实时反映模型性能。
[6]:
def train_single_step(step, config, lr, train_dataset, eval_dataset):
"""train PDE-Net with advancing steps"""
print("Current step for train loop: {}".format(step, ))
model = init_model(config)
epoch = config["epochs"]
warm_up_epoch_scale = 10
if step == 1:
model.if_fronzen = True
epoch = warm_up_epoch_scale * epoch
elif step == 2:
param_dict = get_param_dic(config["summary_dir"], step - 1, epoch * 10)
load_param_into_net(model, param_dict)
print("Load pre-trained model successfully")
else:
param_dict = get_param_dic(config["summary_dir"], step - 1, epoch)
load_param_into_net(model, param_dict)
print("Load pre-trained model successfully")
optimizer = nn.Adam(model.trainable_params(), learning_rate=Tensor(lr))
problem = UnsteadyFlowWithLoss(model, t_out=step, loss_fn=RelativeRMSELoss(), data_format="NTCHW")
def forward_fn(u0, uT):
loss = problem.get_loss(u0, uT)
return loss
grad_fn = mindspore.value_and_grad(forward_fn, None, optimizer.parameters, has_aux=False)
@jit
def train_step(u0, uT):
loss, grads = grad_fn(u0, uT)
loss = ops.depend(loss, optimizer(grads))
return loss
steps = train_dataset.get_dataset_size()
sink_process = mindspore.data_sink(train_step, train_dataset, sink_size=1)
for cur_epoch in range(epoch):
local_time_beg = time.time()
model.set_train()
for _ in range(steps):
cur_loss = sink_process()
print("epoch: %s, loss is %s" % (cur_epoch + 1, cur_loss), flush=True)
local_time_end = time.time()
epoch_seconds = (local_time_end - local_time_beg) * 1000
step_seconds = epoch_seconds / steps
print("Train epoch time: {:5.3f} ms, per step time: {:5.3f} ms".format
(epoch_seconds, step_seconds), flush=True)
if (cur_epoch + 1) % config["save_epoch_interval"] == 0:
ckpt_file_name = "ckpt/step_{}".format(step)
ckpt_dir = os.path.join(config["summary_dir"], ckpt_file_name)
if not os.path.exists(ckpt_dir):
make_dir(ckpt_dir)
ckpt_name = "pdenet-{}.ckpt".format(cur_epoch + 1, )
mindspore.save_checkpoint(model, os.path.join(ckpt_dir, ckpt_name))
if (cur_epoch + 1) % config['eval_interval'] == 0:
calculate_lp_loss_error(problem, eval_dataset, config["batch_size"])
多步训练
PDE-Net是逐步进行训练。 使用MindSpore>= 2.0.0的版本,可以使用函数式编程范式训练神经网络。
[7]:
def train(config):
lr = config["lr"]
for i in range(1, config["multi_step"] + 1):
db_name = "train_step{}.mindrecord".format(i)
dataset = create_dataset(config, i, db_name, "train", data_size=2 * config["batch_size"])
train_dataset, eval_dataset = dataset.create_train_dataset()
lr = scheduler(int(config["multi_step"] / config["learning_rate_reduce_times"]), step=i, lr=lr)
train_single_step(step=i, config=config, lr=lr, train_dataset=train_dataset, eval_dataset=eval_dataset)
[8]:
if not os.path.exists(config["mindrecord_data_dir"]):
make_dir(config["mindrecord_data_dir"])
train(config)
Mindrecorder saved
Current step for train loop: 1
epoch: 1, loss is 313.45258
Train epoch time: 7294.444 ms, per step time: 7294.444 ms
epoch: 2, loss is 283.09055
Train epoch time: 15.857 ms, per step time: 15.857 ms
epoch: 3, loss is 292.2815
Train epoch time: 16.684 ms, per step time: 16.684 ms
epoch: 4, loss is 300.3354
Train epoch time: 18.559 ms, per step time: 18.559 ms
epoch: 5, loss is 295.53436
Train epoch time: 16.430 ms, per step time: 16.430 ms
epoch: 6, loss is 289.45068
Train epoch time: 8.752 ms, per step time: 8.752 ms
epoch: 7, loss is 297.86658
Train epoch time: 10.015 ms, per step time: 10.015 ms
epoch: 8, loss is 269.71762
Train epoch time: 9.050 ms, per step time: 9.050 ms
epoch: 9, loss is 298.23706
Train epoch time: 8.361 ms, per step time: 8.361 ms
epoch: 10, loss is 271.063
Train epoch time: 8.056 ms, per step time: 8.056 ms
================================Start Evaluation================================
LpLoss_error: 15.921201
=================================End Evaluation=================================
...
predict total time: 0.6082212924957275 s
epoch: 491, loss is 0.6402923
Train epoch time: 135.562 ms, per step time: 135.562 ms
epoch: 492, loss is 0.64142
Train epoch time: 115.278 ms, per step time: 115.278 ms
epoch: 493, loss is 0.61553574
Train epoch time: 119.042 ms, per step time: 119.042 ms
epoch: 494, loss is 0.644715
Train epoch time: 111.061 ms, per step time: 111.061 ms
epoch: 495, loss is 0.64503396
Train epoch time: 120.771 ms, per step time: 120.771 ms
epoch: 496, loss is 0.6481593
Train epoch time: 111.252 ms, per step time: 111.252 ms
epoch: 497, loss is 0.6493112
Train epoch time: 110.378 ms, per step time: 110.378 ms
epoch: 498, loss is 0.6368339
Train epoch time: 111.505 ms, per step time: 111.505 ms
epoch: 499, loss is 0.6521274
Train epoch time: 113.217 ms, per step time: 113.217 ms
epoch: 500, loss is 0.65510833
Train epoch time: 115.729 ms, per step time: 115.729 ms
================================Start Evaluation================================
LpLoss_error: 0.040348217
=================================End Evaluation=================================
predict total time: 0.6067502498626709 s
模型推理及可视化
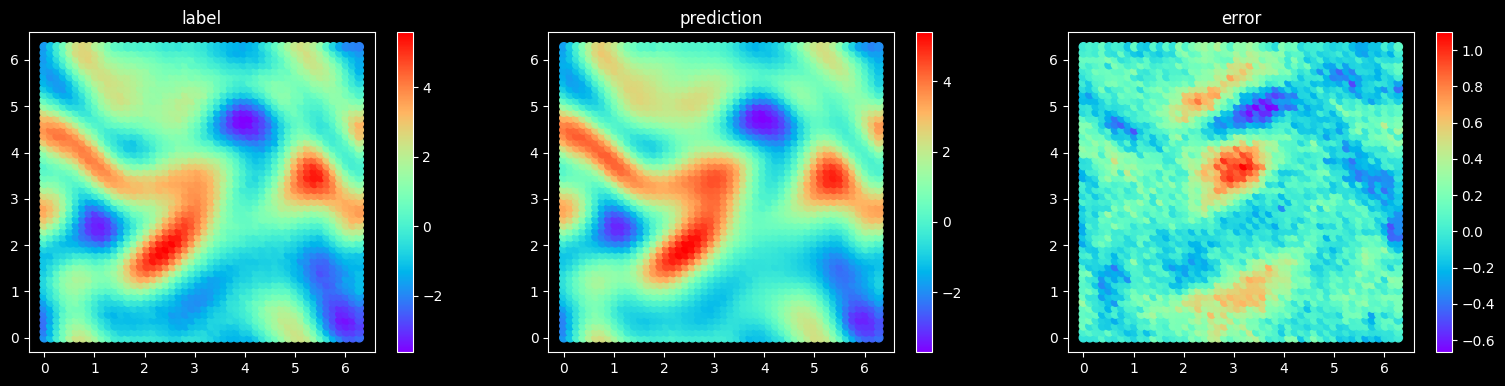
完成训练后,下图展示了预测结果和真实标签的对比情况。
[9]:
step = 20
test_data_size = 20
model = init_model(config)
param_dict = get_param_dic(config["summary_dir"], config["multi_step"], config["epochs"])
load_param_into_net(model, param_dict)
[9]:
[]
Plot Coefficient
[10]:
coe_label = get_label_coe(max_order=config["max_order"], resolution=config["mesh_size"])
coes_out_dir = os.path.join(config["figure_out_dir"], "coes")
plot_coe(model.coe, coes_out_dir, prefix="coe_trained", step=step, title="Coefficient Regression Results of the PDE")
plot_coe(coe_label, coes_out_dir, prefix="coe_label", title="Data Labels for the Coefficients of the PDE")
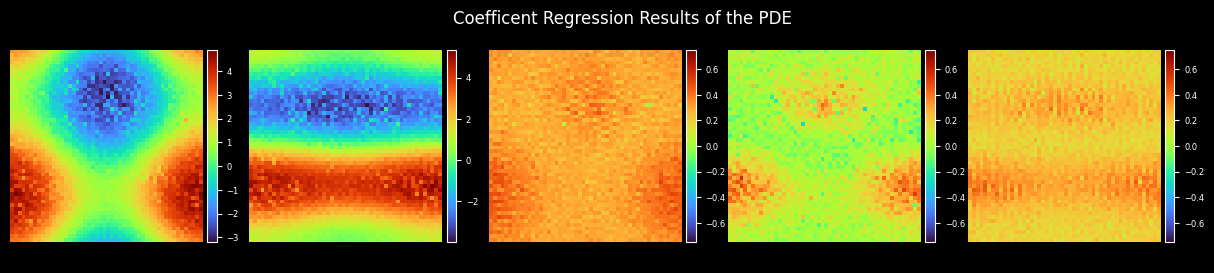
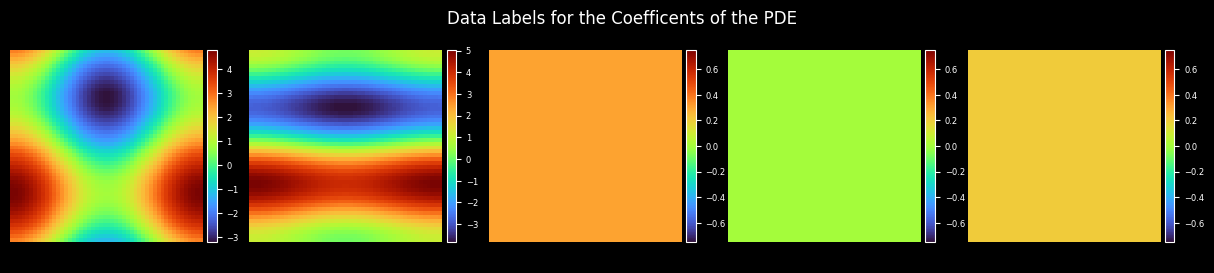
Plot Test Error
[11]:
dataset = create_dataset(config, step, "eval.mindrecord", "test", data_size=test_data_size)
test_dataset = dataset.create_test_dataset(step)
iterator_test_dataset = test_dataset.create_dict_iterator()
final_item = [_ for _ in iterator_test_dataset][-1]
plot_test_error(model, get_loss_metric("mse"), final_item, step, config["mesh_size"], config["figure_out_dir"])
Mindrecorder saved
sample 20, MSE Loss 0.061236363
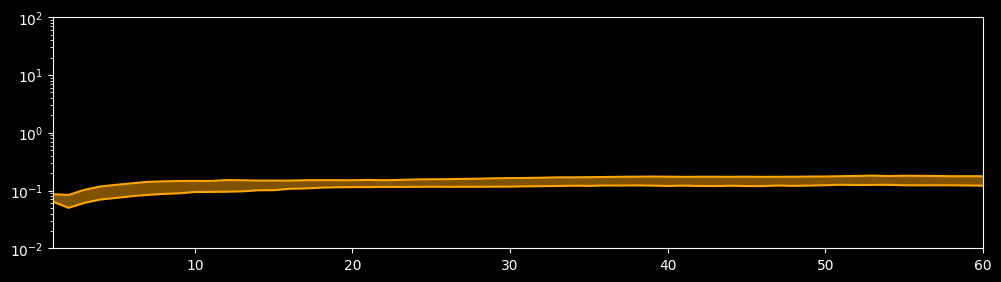
Plot Extrapolation Error
[12]:
max_step = 60
sample_size = 40
dataset = create_dataset(config, max_step, "extrapolation.mindrecord", "test", data_size=sample_size)
plot_extrapolation_error(config, dataset, max_step=max_step)
Mindrecorder saved
step = 1, p25 = 0.06405, p75 = 0.08643
step = 2, p25 = 0.05012, p75 = 0.08393
step = 3, p25 = 0.06112, p75 = 0.10304
step = 4, p25 = 0.06977, p75 = 0.11740
step = 5, p25 = 0.07448, p75 = 0.12558
step = 6, p25 = 0.07964, p75 = 0.13329
step = 7, p25 = 0.08389, p75 = 0.14144
step = 8, p25 = 0.08721, p75 = 0.14411
step = 9, p25 = 0.08933, p75 = 0.14618
step = 10, p25 = 0.09413, p75 = 0.14660
step = 11, p25 = 0.09456, p75 = 0.14647
step = 12, p25 = 0.09532, p75 = 0.15166
step = 13, p25 = 0.09663, p75 = 0.15069
step = 14, p25 = 0.10087, p75 = 0.14878
step = 15, p25 = 0.10134, p75 = 0.14877
step = 16, p25 = 0.10700, p75 = 0.14848
step = 17, p25 = 0.10862, p75 = 0.15084
step = 18, p25 = 0.11188, p75 = 0.15105
step = 19, p25 = 0.11380, p75 = 0.15106
step = 20, p25 = 0.11437, p75 = 0.15068
step = 21, p25 = 0.11436, p75 = 0.15261
step = 22, p25 = 0.11572, p75 = 0.15087
step = 23, p25 = 0.11534, p75 = 0.15267
step = 24, p25 = 0.11588, p75 = 0.15540
step = 25, p25 = 0.11642, p75 = 0.15679
step = 26, p25 = 0.11598, p75 = 0.15700
step = 27, p25 = 0.11619, p75 = 0.15895
step = 28, p25 = 0.11611, p75 = 0.16042
step = 29, p25 = 0.11668, p75 = 0.16299
step = 30, p25 = 0.11663, p75 = 0.16413
step = 31, p25 = 0.11826, p75 = 0.16518
step = 32, p25 = 0.11898, p75 = 0.16673
step = 33, p25 = 0.11977, p75 = 0.16929
step = 34, p25 = 0.12110, p75 = 0.16919
step = 35, p25 = 0.12041, p75 = 0.17030
step = 36, p25 = 0.12223, p75 = 0.17150
step = 37, p25 = 0.12190, p75 = 0.17301
step = 38, p25 = 0.12270, p75 = 0.17389
step = 39, p25 = 0.12147, p75 = 0.17460
step = 40, p25 = 0.12005, p75 = 0.17384
step = 41, p25 = 0.12144, p75 = 0.17257
step = 42, p25 = 0.11986, p75 = 0.17334
step = 43, p25 = 0.11940, p75 = 0.17336
step = 44, p25 = 0.12085, p75 = 0.17301
step = 45, p25 = 0.11940, p75 = 0.17372
step = 46, p25 = 0.11919, p75 = 0.17274
step = 47, p25 = 0.12200, p75 = 0.17317
step = 48, p25 = 0.12044, p75 = 0.17336
step = 49, p25 = 0.12178, p75 = 0.17478
step = 50, p25 = 0.12355, p75 = 0.17511
step = 51, p25 = 0.12578, p75 = 0.17709
step = 52, p25 = 0.12434, p75 = 0.17895
step = 53, p25 = 0.12512, p75 = 0.18118
step = 54, p25 = 0.12532, p75 = 0.17828
step = 55, p25 = 0.12323, p75 = 0.18043
step = 56, p25 = 0.12300, p75 = 0.17973
step = 57, p25 = 0.12319, p75 = 0.17869
step = 58, p25 = 0.12315, p75 = 0.17695
step = 59, p25 = 0.12245, p75 = 0.17721
step = 60, p25 = 0.12120, p75 = 0.17679